3. Description of the Catalogue

3.1. Which global constraints are included?
3.2. Which global constraints are missing?
3.3. Searching in the catalogue
3.4. Figures of the catalogue
3.5. Constraints argument patterns
- 3.5.1. Constraints with 1 argument
- 3.5.2. Constraints with 2 arguments
- 3.5.3. Constraints with 3 arguments
- 3.5.4. Constraints with 4 arguments
- 3.5.5. Constraints with 5 arguments
- 3.5.6. Constraints with 6 arguments
- 3.5.7. Constraints with 8 arguments
- 3.5.8. Constraints with 10 arguments
3.6. Meta-keywords attached to the keywords
- 3.6.1. Application area
- 3.6.2. Characteristic of a constraint
- 3.6.3. Combinatorial object
- 3.6.4. Complexity
- 3.6.5. Constraint network structure
- 3.6.6. Constraint type
- 3.6.7. Constraint arguments
- 3.6.8. Filtering
- 3.6.9. Final graph structure
- 3.6.10. Geometry
- 3.6.11. Heuristics
- 3.6.12. Miscellaneous
- 3.6.13. Modelling
- 3.6.14. Modelling exercises
- 3.6.15. Problems
- 3.6.16. Puzzles
- 3.6.17. Symmetry
3.7. Keywords attached to the global constraints
- 3.7.1. 3-dimensional-matching
- 3.7.2. 3-SAT
- 3.7.3. Abstract interpretation
- 3.7.4. Acyclic
- 3.7.5. Aggregate
- 3.7.6. Air traffic management
- 3.7.7. Alignment
- 3.7.8. All different
- 3.7.9. Alpha-acyclic constraint network(2)
- 3.7.10. Alpha-acyclic constraint network(3)
- 3.7.11. Apartition
- 3.7.12. Arc-consistency
- 3.7.13. Arithmetic constraint
- 3.7.14. Array constraint
- 3.7.15. Assigning and scheduling tasks that run in parallel
- 3.7.16. Assignment
- 3.7.17. Assignment dimension
- 3.7.18. Assignment to the same set of values
- 3.7.19. At least
- 3.7.20. At most
- 3.7.21. Automaton
- 3.7.22. Automaton with array of counters
- 3.7.23. Automaton with counters
- 3.7.24. Automaton with same input symbol
- 3.7.25. Automaton without counters
- 3.7.26. Autoref
- 3.7.27. Balanced assignment
- 3.7.28. Balanced tree
- 3.7.29. Berge-acyclic constraint network
- 3.7.30. Binary constraint
- 3.7.31. Bioinformatics
- 3.7.32. Bipartite
- 3.7.33. Bipartite matching
- 3.7.34. Bipartite matching in convex bipartite graphs
- 3.7.35. Boolean channel
- 3.7.36. Boolean constraint
- 3.7.37. Border
- 3.7.38. Bound-consistency
- 3.7.39. Business rules
- 3.7.40. Centered cyclic(1) constraint network(1)
- 3.7.41. Centered cyclic(2) constraint network(1)
- 3.7.42. Centered cyclic(3) constraint network(1)
- 3.7.43. Channel routing
- 3.7.44. Channelling constraint
- 3.7.45. Circuit
- 3.7.46. Circular sliding cyclic(1) constraint network(2)
- 3.7.47. Cluster
- 3.7.48. Coloured
- 3.7.49. Compulsory part
- 3.7.50. Conditional constraint
- 3.7.51. Configuration problem
- 3.7.52. Connected component
- 3.7.53. Consecutive loops are connected
- 3.7.54. Consecutive values
- 3.7.55. Constraint between two collections of variables
- 3.7.56. Constraint between three collections of variables
- 3.7.57. Constraint involving set variables
- 3.7.58. Constraint on the intersection
- 3.7.59. Constructive disjunction
- 3.7.60. Contact
- 3.7.61. Contractible
- 3.7.62. Convex
- 3.7.63. Convex bipartite graph
- 3.7.64. Convex hull relaxation
- 3.7.65. Conway packing problem
- 3.7.66. Core
- 3.7.67. Costas arrays
- 3.7.68. Cost filtering constraint
- 3.7.69. Cost matrix
- 3.7.70. Counting constraint
- 3.7.71. Cumulative longest hole problems
- 3.7.72. Cycle
- 3.7.73. Cyclic
- 3.7.74. Data constraint
- 3.7.75. Deadlock breaking
- 3.7.76. Decomposition
- 3.7.77. Decomposition-based violation measure
- 3.7.78. Demand profile
- 3.7.79. Degree of diversity of a set of solutions
- 3.7.80. Derived collection
- 3.7.81. DFS-bottleneck
- 3.7.82. Difference
- 3.7.83. Difference between pairs of variables
- 3.7.84. Directed acyclic graph
- 3.7.85. Disequality
- 3.7.86. Disjunction
- 3.7.87. Domain channel
- 3.7.88. Domain definition
- 3.7.89. Dominating queens
- 3.7.90. Domination
- 3.7.91. Dual model
- 3.7.92. Duplicated variables
- 3.7.93. Dynamic programming
- 3.7.94. Empty intersection
- 3.7.95. Entailment
- 3.7.96. Equality
- 3.7.97. Equality between multisets
- 3.7.98. Equivalence
- 3.7.99. Euler knight
- 3.7.100. Excluded
- 3.7.101. Extensible
- 3.7.102. Extension
- 3.7.103. Facilities location problem
- 3.7.104. Floor planning problem
- 3.7.105. Flow
- 3.7.106. Frequency allocation problem
- 3.7.107. Functional dependency
- 3.7.108. Geometrical constraint
- 3.7.109. Glue matrix
- 3.7.110. Golomb ruler
- 3.7.111. Graph colouring
- 3.7.112. Graph constraint
- 3.7.113. Graph partitioning constraint
- 3.7.114. Guillotine cut
- 3.7.115. Hall interval
- 3.7.116. Hamiltonian
- 3.7.117. Heuristics
- 3.7.118. Heuristics and Berge-acyclic constraint network
- 3.7.119. Heuristics and lexicographical ordering
- 3.7.120. Heuristics for two-dimensional rectangle placement problems
  - 3.7.120.1. Dual strategy for rectangle placement problems with no slack
  - 3.7.120.2. Strategy that gradually creates a compulsory part
- 3.7.121. Hungarian method for the assignment problem
- 3.7.122. Hybrid-consistency
- 3.7.123. Hypergraph
- 3.7.124. Included
- 3.7.125. Inclusion
- 3.7.126. Incompatible pairs of values
- 3.7.127. Indistinguishable values
- 3.7.128. Interval
- 3.7.129. Involution
- 3.7.130. Joker value
- 3.7.131. Klee's measure problem
- 3.7.132. Labelling by increasing cost
- 3.7.133. Latin square
- 3.7.134. Lexicographic order
- 3.7.135. Limited discrepancy search
- 3.7.136. Linear programming
- 3.7.137. Line segments intersection
- 3.7.138. Logic
- 3.7.139. Logigraphe
- 3.7.140. Magic hexagon
- 3.7.141. Magic series
- 3.7.142. Magic square
- 3.7.143. Matching
- 3.7.144. Matrix
- 3.7.145. Matrix model
- 3.7.146. Matrix symmetry
- 3.7.147. Maximum
- 3.7.148. Maximum clique
- 3.7.149. Maximum number of occurrences
- 3.7.150. maxint
- 3.7.151. Metro
- 3.7.152. Minimum
- 3.7.153. Minimum cost flow
- 3.7.154. Minimum feedback vertex set
- 3.7.155. Minimum hitting set cardinality
- 3.7.156. Minimum number of occurrences
- 3.7.157. Modulo
- 3.7.158. Multi-site employee scheduling with calendar constraints
- 3.7.159. Multiset
- 3.7.160. Multiset ordering
- 3.7.161. No cycle
- 3.7.162. No loop
- 3.7.163. n-Amazons
- 3.7.164. n-queens
- 3.7.165. Non-deterministic automaton
- 3.7.166. Non-overlapping
- 3.7.167. Number of changes
- 3.7.168. Number of distinct equivalence classes
- 3.7.169. Number of distinct values
- 3.7.170. Obscure
- 3.7.171. One succ
- 3.7.172. Open automaton constraint
- 3.7.173. Open constraint
- 3.7.174. Order constraint
- 3.7.175. Orthotope
- 3.7.176. Overlapping alldifferent
- 3.7.177. Pair
- 3.7.178. Packing almost squares
- 3.7.179. Pallet loading
- 3.7.180. Partition
- 3.7.181. Path
- 3.7.182. Partridge
- 3.7.183. Pattern sequencing
- 3.7.184. Pentomino
- 3.7.185. Periodic
- 3.7.186. Permutation
- 3.7.187. Permutation channel
- 3.7.188. Phi-tree
- 3.7.189. Phylogeny
- 3.7.190. Pick-up delivery
- 3.7.191. Planarity test
- 3.7.192. Polygon
- 3.7.193. Positioning constraint
- 3.7.194. Predefined constraint
- 3.7.195. Preferences
- 3.7.196. Producer-consumer
- 3.7.197. Product
- 3.7.198. Program verification
- 3.7.199. Proximity constraint
- 3.7.200. Pure functional dependency
- 3.7.201. Quadtree
- 3.7.202. Range
- 3.7.203. Rank
- 3.7.204. RCC8
- 3.7.205. Rectangle clique partition
- 3.7.206. Regret based heuristics
- 3.7.207. Regret based heuristics in matrix problems
- 3.7.208. Reified automaton constraint
- 3.7.209. Reified constraint
- 3.7.210. Relation
- 3.7.211. Relaxation
- 3.7.212. Relaxation dimension
- 3.7.213. Resource constraint
- 3.7.214. Reverse of a constraint
- 3.7.215. Run of a permutation
- 3.7.216. SAT
- 3.7.217. Scalar product
- 3.7.218. Sequence
- 3.7.219. Sequence dependent set-up
- 3.7.220. Sequencing with release times and deadlines
- 3.7.221. Set channel
- 3.7.222. Set packing
- 3.7.223. Shikaku
- 3.7.224. Scheduling constraint
- 3.7.225. Scheduling with machine choice, calendars and preemption
- 3.7.226. Shared table
- 3.7.227. Schur number
- 3.7.228. SLAM problem
- 3.7.229. Sliding cyclic(1) constraint network(1)
- 3.7.230. Sliding cyclic(1) constraint network(2)
- 3.7.231. Sliding cyclic(1) constraint network(3)
- 3.7.232. Sliding cyclic(2) constraint network(2)
- 3.7.233. Sliding sequence constraint
- 3.7.234. Smallest square for packing consecutive dominoes
- 3.7.235. Smallest rectangle area
- 3.7.236. Smallest square for packing rectangles with distinct sizes
- 3.7.237. Soft constraint
- 3.7.238. Sort
- 3.7.239. Sort based reformulation
- 3.7.240. Sparse functional dependency
- 3.7.241. Sparse table
- 3.7.242. Sport timetabling
- 3.7.243. Squared squares
- 3.7.244. Statistics
- 3.7.245. Strip packing
- 3.7.246. Strong articulation point
- 3.7.247. Strong bridge
- 3.7.248. Strongly connected component
- 3.7.249. Subset sum
- 3.7.250. Sudoku
- 3.7.251. Sum
- 3.7.252. Sweep
- 3.7.253. Symmetric
- 3.7.254. Symmetry
- 3.7.255. System of constraints
- 3.7.256. Table
- 3.7.257. Temporal constraint
- 3.7.258. Ternary constraint
- 3.7.259. Timetabling constraint
- 3.7.260. Time window
- 3.7.261. Touch
- 3.7.262. Tree
- 3.7.263. Tuple
- 3.7.264. Two-dimensional orthogonal packing
- 3.7.265. Unary constraint
- 3.7.266. Undirected graph
- 3.7.267. Value constraint
- 3.7.268. Value partitioning constraint
- 3.7.269. Value precedence
- 3.7.270. Variable-based violation measure
- 3.7.271. Variable indexing
- 3.7.272. Variable subscript
- 3.7.273. Vector
- 3.7.274. Vpartition
- 3.7.275. Weighted assignment
- 3.7.276. Workload covering
- 3.7.277. Zebra puzzle
- 3.7.278. Zero-duration task

3.7.234. Smallest square for packing consecutive dominoes

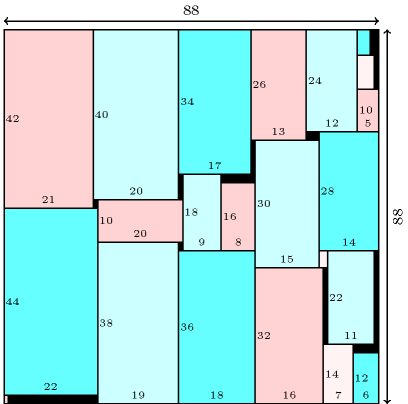
Find the smallest square $S$ where one can place $n$ rectangles of respective size $1 \times 2, 2 \times 4, \dots, n \times 2 \cdot n$ so that they do not overlap and so that their borders are parallel to the borders of $S$ . Each rectangle can be rotated by 90 degrees. The problem is described in http://www.stetson.edu/~efriedma/domino/. Figure 3.7.65 gives a solution for $n = 22$ found by H. Simonis.

Figure 3.7.65. A solution to the smallest square for packing consecutive dominoes problem for $n = 22$

Global Constraint Catalog

3. Description of the Catalogue

3.7.234. Smallest square for packing consecutive dominoes

Figure 3.7.65. A solution to the smallest square for packing consecutive dominoes problem for n=22

Figure 3.7.65. A solution to the smallest square for packing consecutive dominoes problem for $n = 22$