Global Constraint Catalog: Cconsecutive_groups_of

5.87. consecutive_groups_of_ones

DESCRIPTION

LINKS

AUTOMATON

Origin

Derived from $𝚐𝚛𝚘𝚞𝚙$

Constraint

$𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚐𝚛𝚘𝚞𝚙𝚜_𝚘𝚏_𝚘𝚗𝚎𝚜 (𝙶𝚁𝙾𝚄𝙿_𝚂𝙸𝚉𝙴𝚂, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Arguments

$𝙶𝚁𝙾𝚄𝙿_𝚂𝙸𝚉𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚗𝚋 - 𝚒𝚗𝚝)$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝙶𝚁𝙾𝚄𝙿_𝚂𝙸𝚉𝙴𝚂, 𝚗𝚋)

| 𝙶𝚁𝙾𝚄𝙿_𝚂𝙸𝚉𝙴𝚂 | \geq 1

𝙶𝚁𝙾𝚄𝙿_𝚂𝙸𝚉𝙴𝚂 . 𝚗𝚋 \geq 1

𝙶𝚁𝙾𝚄𝙿_𝚂𝙸𝚉𝙴𝚂 . 𝚗𝚋 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | \geq 2 * | 𝙶𝚁𝙾𝚄𝙿_𝚂𝙸𝚉𝙴𝚂 | - 1

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | \geq

𝚜𝚞𝚖

(𝙶𝚁𝙾𝚄𝙿_𝚂𝙸𝚉𝙴𝚂 . 𝚗𝚋) + | 𝙶𝚁𝙾𝚄𝙿_𝚂𝙸𝚉𝙴𝚂 | - 1

𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛 \geq 0

𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛 \leq 1

Purpose

In order to define the meaning of the $𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚐𝚛𝚘𝚞𝚙𝚜_𝚘𝚏_𝚘𝚗𝚎𝚜$ constraint, we first introduce the notions of stretch and span. Let $n$ be the number of variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ and let $m$ be the number of items of the collection $𝙶𝚁𝙾𝚄𝙿_𝚂𝙸𝚉𝙴𝚂$ . Let $X_{i}, \dots, X_{j}$ $(1 \leq i \leq j \leq n)$ be consecutive variables of the collection of variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ such that the following conditions apply:

All variables $X_{i}, \dots, X_{j}$ are assigned value 1,
$i = 1$ or $X_{i - 1} \neq 1$ ,
$j = n$ or $X_{j + 1} \neq 1$ .

We call such a set of variables a stretch. The span of the stretch is equal to $j - i + 1$ . We now define the condition enforced by the $𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚐𝚛𝚘𝚞𝚙𝚜_𝚘𝚏_𝚘𝚗𝚎𝚜$ constraint.

All variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection should be assigned value 0 or 1. In addition there is $| 𝙶𝚁𝙾𝚄𝙿_𝚂𝙸𝚉𝙴𝚂 |$ successive stretches of respective span $𝙶𝚁𝙾𝚄𝙿_𝚂𝙸𝚉𝙴𝚂 [1] . 𝚗𝚋,$ $𝙶𝚁𝙾𝚄𝙿_𝚂𝙸𝚉𝙴𝚂 [2] . 𝚗𝚋, \dots,$ $𝙶𝚁𝙾𝚄𝙿_𝚂𝙸𝚉𝙴𝚂 [m] . 𝚗𝚋$ .

Example

(〈2, 1〉, 〈1, 1, 0, 0, 0, 1, 0〉)

The $𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚐𝚛𝚘𝚞𝚙𝚜_𝚘𝚏_𝚘𝚗𝚎𝚜$ constraint holds since the sequence $1100010$ contains a first stretch (i.e., a maximum sequence of 1) of span 2 and a second stretch of span 1.

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 1

Symmetry

Items of $𝙶𝚁𝙾𝚄𝙿_𝚂𝙸𝚉𝙴𝚂$ and $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are simultaneously reversable.

Usage

The $𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚐𝚛𝚘𝚞𝚙𝚜_𝚘𝚏_𝚘𝚗𝚎𝚜$ constraint can be used in order to model the logigraphe problem.

See also

root concept: $𝚐𝚛𝚘𝚞𝚙$ .

Keywords

characteristic of a constraint: automaton, automaton without counters, reified automaton constraint.

constraint network structure: Berge-acyclic constraint network.

filtering: arc-consistency.

modelling exercises: logigraphe.

puzzles: logigraphe.

Automaton: Figure 5.87.1 depicts the automaton associated with the $𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚐𝚛𝚘𝚞𝚙𝚜_𝚘𝚏_𝚘𝚗𝚎𝚜$ constraint. To each variable ${𝚅𝙰𝚁}_{i}$ of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ corresponds a signature variable that is equal to ${𝚅𝙰𝚁}_{i}$ . There is no signature constraint.

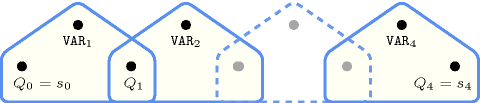
Figure 5.87.1. Non deterministic automaton of the $𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚐𝚛𝚘𝚞𝚙𝚜_𝚘𝚏_𝚘𝚗𝚎𝚜$ constraint of the Example slot (a stretch of two 1 followed by a stretch of a single 1)

Figure 5.87.2. Hypergraph of the reformulation corresponding to the automaton of the $𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚐𝚛𝚘𝚞𝚙𝚜_𝚘𝚏_𝚘𝚗𝚎𝚜$ constraint of the Example slot

Global Constraint Catalog

5. Global Constraint Catalogue

5.87. consecutive_groups_of_ones

Figure 5.87.1. Non deterministic automaton of the $𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚐𝚛𝚘𝚞𝚙𝚜_𝚘𝚏_𝚘𝚗𝚎𝚜$ constraint of the Example slot (a stretch of two 1 followed by a stretch of a single 1)

Figure 5.87.2. Hypergraph of the reformulation corresponding to the automaton of the $𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚐𝚛𝚘𝚞𝚙𝚜_𝚘𝚏_𝚘𝚗𝚎𝚜$ constraint of the Example slot

Global Constraint Catalog

5. Global Constraint Catalogue

5.87. consecutive_groups_of_ones

Figure 5.87.1. Non deterministic automaton of the 𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚐𝚛𝚘𝚞𝚙𝚜_𝚘𝚏_𝚘𝚗𝚎𝚜 constraint of the Example slot (a stretch of two 1 followed by a stretch of a single 1)

Figure 5.87.2. Hypergraph of the reformulation corresponding to the automaton of the 𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚐𝚛𝚘𝚞𝚙𝚜_𝚘𝚏_𝚘𝚗𝚎𝚜 constraint of the Example slot

Figure 5.87.1. Non deterministic automaton of the $𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚐𝚛𝚘𝚞𝚙𝚜_𝚘𝚏_𝚘𝚗𝚎𝚜$ constraint of the Example slot (a stretch of two 1 followed by a stretch of a single 1)

Figure 5.87.2. Hypergraph of the reformulation corresponding to the automaton of the $𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚐𝚛𝚘𝚞𝚙𝚜_𝚘𝚏_𝚘𝚗𝚎𝚜$ constraint of the Example slot