Global Constraint Catalog: Cgeost

5.159. geost

DESCRIPTION

LINKS

Origin

Constraint

$𝚐𝚎𝚘𝚜𝚝 (𝙺, 𝙾𝙱𝙹𝙴𝙲𝚃𝚂, 𝚂𝙱𝙾𝚇𝙴𝚂)$

Types

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟 - 𝚍𝚟𝚊𝚛)$
$𝙸𝙽𝚃𝙴𝙶𝙴𝚁𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟 - 𝚒𝚗𝚝)$
$𝙿𝙾𝚂𝙸𝚃𝙸𝚅𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟 - 𝚒𝚗𝚝)$

Arguments

$𝙺$	$𝚒𝚗𝚝$
$𝙾𝙱𝙹𝙴𝙲𝚃𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚘𝚒𝚍 - 𝚒𝚗𝚝, 𝚜𝚒𝚍 - 𝚍𝚟𝚊𝚛, 𝚡 - 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$
$𝚂𝙱𝙾𝚇𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚜𝚒𝚍 - 𝚒𝚗𝚝, 𝚝 - 𝙸𝙽𝚃𝙴𝙶𝙴𝚁𝚂, 𝚕 - 𝙿𝙾𝚂𝙸𝚃𝙸𝚅𝙴𝚂)$

Restrictions

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | \geq 1

| 𝙸𝙽𝚃𝙴𝙶𝙴𝚁𝚂 | \geq 1

| 𝙿𝙾𝚂𝙸𝚃𝙸𝚅𝙴𝚂 | \geq 1

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟)

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | = 𝙺

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝙸𝙽𝚃𝙴𝙶𝙴𝚁𝚂, 𝚟)

| 𝙸𝙽𝚃𝙴𝙶𝙴𝚁𝚂 | = 𝙺

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝙿𝙾𝚂𝙸𝚃𝙸𝚅𝙴𝚂, 𝚟)

| 𝙿𝙾𝚂𝙸𝚃𝙸𝚅𝙴𝚂 | = 𝙺

𝙿𝙾𝚂𝙸𝚃𝙸𝚅𝙴𝚂 . 𝚟 > 0

𝙺 > 0

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝙾𝙱𝙹𝙴𝙲𝚃𝚂, [𝚘𝚒𝚍, 𝚜𝚒𝚍, 𝚡])

𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝

(𝙾𝙱𝙹𝙴𝙲𝚃𝚂, 𝚘𝚒𝚍)

𝙾𝙱𝙹𝙴𝙲𝚃𝚂 . 𝚘𝚒𝚍 \geq 1

𝙾𝙱𝙹𝙴𝙲𝚃𝚂 . 𝚘𝚒𝚍 \leq | 𝙾𝙱𝙹𝙴𝙲𝚃𝚂 |

𝙾𝙱𝙹𝙴𝙲𝚃𝚂 . 𝚜𝚒𝚍 \geq 1

𝙾𝙱𝙹𝙴𝙲𝚃𝚂 . 𝚜𝚒𝚍 \leq | 𝚂𝙱𝙾𝚇𝙴𝚂 |

| 𝚂𝙱𝙾𝚇𝙴𝚂 | \geq 1

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚂𝙱𝙾𝚇𝙴𝚂, [𝚜𝚒𝚍, 𝚝, 𝚕])

𝚂𝙱𝙾𝚇𝙴𝚂 . 𝚜𝚒𝚍 \geq 1

𝚂𝙱𝙾𝚇𝙴𝚂 . 𝚜𝚒𝚍 \leq | 𝚂𝙱𝙾𝚇𝙴𝚂 |

𝚍𝚘_𝚗𝚘𝚝_𝚘𝚟𝚎𝚛𝚕𝚊𝚙 (𝚂𝙱𝙾𝚇𝙴𝚂)

Purpose

Holds if, for each pair of objects $(O_{i}, O_{j})$ , $i < j$ , $O_{i}$ and $O_{j}$ do not overlap with respect to a set of dimensions ${1, 2, \dots, 𝙺}$ . $O_{i}$ and $O_{j}$ are objects that take a shape among a set of shapes. Each shape is defined as a finite set of shifted boxes, where each shifted box is described by a box in a $𝙺$ -dimensional space at a given offset (from the origin of the shape) with given sizes that are all strictly greater than 0. More precisely, a shifted box is an entity defined by its shape id $𝚜𝚒𝚍$ , shift offset $𝚝$ , and sizes $𝚕$ . Then, a shape is defined as the union of shifted boxes sharing the same shape id. An object is an entity defined by its unique object identifier $𝚘𝚒𝚍$ , shape id $𝚜𝚒𝚍$ and origin $𝚡$ .

An object $O_{i}$ does not overlap an object $O_{j}$ with respect to the set of dimensions ${1, 2, \dots, 𝙺}$ if and only if for all shifted box $s_{i}$ associated with $O_{i}$ and for all shifted box $s_{j}$ associated with $O_{j}$ there exists a dimension $d \in {1, 2, \dots, 𝙺}$ such that the start of $s_{i}$ in dimension $d$ is greater than or equal to the end of $s_{j}$ in dimension $d$ , or the start of $s_{j}$ in dimension $d$ is greater than or equal to the end of $s_{i}$ in dimension $d$ .

Example

(\begin{matrix} 2, 〈\begin{matrix} 𝚘𝚒𝚍 - 1 & 𝚜𝚒𝚍 - 1 & 𝚡 - 〈1, 2〉, \\ 𝚘𝚒𝚍 - 2 & 𝚜𝚒𝚍 - 5 & 𝚡 - 〈2, 1〉, \\ 𝚘𝚒𝚍 - 3 & 𝚜𝚒𝚍 - 8 & 𝚡 - 〈4, 1〉 \end{matrix}〉, \\ 〈\begin{matrix} 𝚜𝚒𝚍 - 1 & 𝚝 - 〈0, 0〉 & 𝚕 - 〈2, 1〉, \\ 𝚜𝚒𝚍 - 1 & 𝚝 - 〈0, 1〉 & 𝚕 - 〈1, 2〉, \\ 𝚜𝚒𝚍 - 1 & 𝚝 - 〈1, 2〉 & 𝚕 - 〈3, 1〉, \\ 𝚜𝚒𝚍 - 2 & 𝚝 - 〈0, 0〉 & 𝚕 - 〈3, 1〉, \\ 𝚜𝚒𝚍 - 2 & 𝚝 - 〈0, 1〉 & 𝚕 - 〈1, 3〉, \\ 𝚜𝚒𝚍 - 2 & 𝚝 - 〈2, 1〉 & 𝚕 - 〈1, 1〉, \\ 𝚜𝚒𝚍 - 3 & 𝚝 - 〈0, 0〉 & 𝚕 - 〈2, 1〉, \\ 𝚜𝚒𝚍 - 3 & 𝚝 - 〈1, 1〉 & 𝚕 - 〈1, 2〉, \\ 𝚜𝚒𝚍 - 3 & 𝚝 - 〈- 2, 2〉 & 𝚕 - 〈3, 1〉, \\ 𝚜𝚒𝚍 - 4 & 𝚝 - 〈0, 0〉 & 𝚕 - 〈3, 1〉, \\ 𝚜𝚒𝚍 - 4 & 𝚝 - 〈0, 1〉 & 𝚕 - 〈1, 1〉, \\ 𝚜𝚒𝚍 - 4 & 𝚝 - 〈2, 1〉 & 𝚕 - 〈1, 3〉, \\ 𝚜𝚒𝚍 - 5 & 𝚝 - 〈0, 0〉 & 𝚕 - 〈2, 1〉, \\ 𝚜𝚒𝚍 - 5 & 𝚝 - 〈1, 1〉 & 𝚕 - 〈1, 1〉, \\ 𝚜𝚒𝚍 - 5 & 𝚝 - 〈0, 2〉 & 𝚕 - 〈2, 1〉, \\ 𝚜𝚒𝚍 - 6 & 𝚝 - 〈0, 0〉 & 𝚕 - 〈3, 1〉, \\ 𝚜𝚒𝚍 - 6 & 𝚝 - 〈0, 1〉 & 𝚕 - 〈1, 1〉, \\ 𝚜𝚒𝚍 - 6 & 𝚝 - 〈2, 1〉 & 𝚕 - 〈1, 1〉, \\ 𝚜𝚒𝚍 - 7 & 𝚝 - 〈0, 0〉 & 𝚕 - 〈3, 2〉, \\ 𝚜𝚒𝚍 - 8 & 𝚝 - 〈0, 0〉 & 𝚕 - 〈2, 3〉 \end{matrix}〉 \end{matrix})

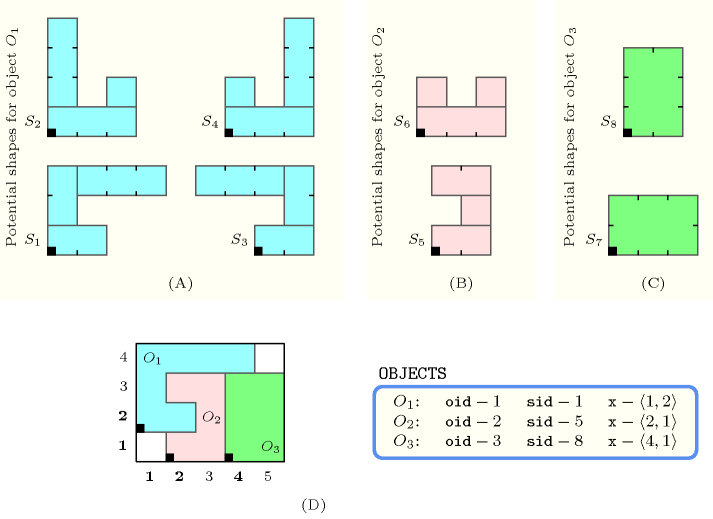
Parts (A), (B) and (C) of Figure 5.159.1 respectively represent the potential shapes associated with the three objects of the example. Part (D) shows the position of the three objects of the example, where the first, second and third objects were respectively assigned shapes 1, 5 and 8. The coordinates of the leftmost lowest corner of each object are stressed in bold. The $𝚐𝚎𝚘𝚜𝚝$ constraint holds since the three objects do not overlap (i.e., see part (D) if Figure 5.159.1).

Figure 5.159.1. (D) The three non-overlapping objects $O_{1}$ , $O_{2}$ , $O_{3}$ of the Example slot respectively assigned shapes $S_{1}$ , $S_{5}$ , $S_{8}$ ; (A), (B), (C) shapes $S_{1}$ , $S_{2}$ , $S_{3}$ , $S_{4}$ , $S_{5}$ , $S_{6}$ , $S_{7}$ and $S_{8}$ are respectively made up from 3, 3, 3, 3, 3, 3, 1 and 1 disjoint shifted box.

Typical

| 𝙾𝙱𝙹𝙴𝙲𝚃𝚂 | > 1

Symmetries

Items of $𝙾𝙱𝙹𝙴𝙲𝚃𝚂$ are permutable.
Items of $𝚂𝙱𝙾𝚇𝙴𝚂$ are permutable.
Items of $𝙾𝙱𝙹𝙴𝙲𝚃𝚂 . 𝚡$ , $𝚂𝙱𝙾𝚇𝙴𝚂 . 𝚝$ and $𝚂𝙱𝙾𝚇𝙴𝚂 . 𝚕$ are permutable (same permutation used).
$𝚂𝙱𝙾𝚇𝙴𝚂 . 𝚕 . 𝚟$ can be decreased to any value $\geq 1$ .

Usage

The $𝚐𝚎𝚘𝚜𝚝$ constraint allows to model directly a large number of placement problems.

Remark

In the two-dimensional case, when rectangles heights are all equal to one and when rectangles starts in the first dimension are all fixed, the $𝚐𝚎𝚘𝚜𝚝$ constraint can be rewritten as a $𝚔_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ constraint corresponding to a system of $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ constraints derived from the maximum cliques of the corresponding interval graph.

Algorithm

A sweep-based filtering algorithm for this constraint is described in [BeldiceanuCarlssonPoderSadekTruchet07]. Unlike previous sweep filtering algorithms which move a line for finding a feasible position for the origin of an object, this algorithm performs a recursive traversal of the multidimensional placement space. It explores all points of the domain of the origin of the object under focus, one by one, in increasing lexicographic order, until a point is found that is not infeasible for any non-overlapping constraints. To make the search efficient, instead of moving each time to the successor point, the search is arranged so that it skips points that are known to be infeasible for some non-overlapping constraint.

Within the context of breaking symmetries six different ways of integrating within $𝚐𝚎𝚘𝚜𝚝$ a chain of lexicographical ordering constraints like $𝚕𝚎𝚡_𝚌𝚑𝚊𝚒𝚗_𝚕𝚎𝚜𝚜$ for enforcing a lexicographic ordering on the origin coordinates of identical objects, are described in [AgrenCarlssonBeldiceanuSbihiTruchetZampelli09].

Systems