Global Constraint Catalog: Corth_on_top_of

5.312. orth_on_top_of_orth

DESCRIPTION

LINKS

GRAPH

Origin

Used for defining $𝚙𝚕𝚊𝚌𝚎_𝚒𝚗_𝚙𝚢𝚛𝚊𝚖𝚒𝚍$ .

Constraint

$𝚘𝚛𝚝𝚑_𝚘𝚗_𝚝𝚘𝚙_𝚘𝚏_𝚘𝚛𝚝𝚑 (𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1, 𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 2, 𝚅𝙴𝚁𝚃𝙸𝙲𝙰𝙻_𝙳𝙸𝙼)$

Type

𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴

𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚘𝚛𝚒 - 𝚍𝚟𝚊𝚛, 𝚜𝚒𝚣 - 𝚍𝚟𝚊𝚛, 𝚎𝚗𝚍 - 𝚍𝚟𝚊𝚛)

Arguments

$𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1$	$𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴$
$𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 2$	$𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴$
$𝚅𝙴𝚁𝚃𝙸𝙲𝙰𝙻_𝙳𝙸𝙼$	$𝚒𝚗𝚝$

Restrictions

| 𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 | > 0

𝚛𝚎𝚚𝚞𝚒𝚛𝚎_𝚊𝚝_𝚕𝚎𝚊𝚜𝚝

(2, 𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴, [𝚘𝚛𝚒, 𝚜𝚒𝚣, 𝚎𝚗𝚍])

𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 . 𝚜𝚒𝚣 \geq 0

𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 . 𝚘𝚛𝚒 \leq 𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 . 𝚎𝚗𝚍

| 𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1 | = | 𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 2 |

𝚅𝙴𝚁𝚃𝙸𝙲𝙰𝙻_𝙳𝙸𝙼 \geq 1

𝚅𝙴𝚁𝚃𝙸𝙲𝙰𝙻_𝙳𝙸𝙼 \leq | 𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1 |

𝚘𝚛𝚝𝚑_𝚕𝚒𝚗𝚔_𝚘𝚛𝚒_𝚜𝚒𝚣_𝚎𝚗𝚍

(𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1)

𝚘𝚛𝚝𝚑_𝚕𝚒𝚗𝚔_𝚘𝚛𝚒_𝚜𝚒𝚣_𝚎𝚗𝚍

(𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 2)

Purpose

$𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1$ is located on top of $𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 2$ which concretely means:

In each dimension different from $𝚅𝙴𝚁𝚃𝙸𝙲𝙰𝙻_𝙳𝙸𝙼$ the projection of $𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1$ is included in the projection of $𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 2$ .
In the dimension $𝚅𝙴𝚁𝚃𝙸𝙲𝙰𝙻_𝙳𝙸𝙼$ the origin of $𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1$ coincide with the end of $𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 2$ .

Example

(\begin{matrix} 〈𝚘𝚛𝚒 - 5 𝚜𝚒𝚣 - 2 𝚎𝚗𝚍 - 7, 𝚘𝚛𝚒 - 3 𝚜𝚒𝚣 - 3 𝚎𝚗𝚍 - 6〉, \\ 〈𝚘𝚛𝚒 - 3 𝚜𝚒𝚣 - 5 𝚎𝚗𝚍 - 8, 𝚘𝚛𝚒 - 1 𝚜𝚒𝚣 - 2 𝚎𝚗𝚍 - 3〉, 2 \end{matrix})

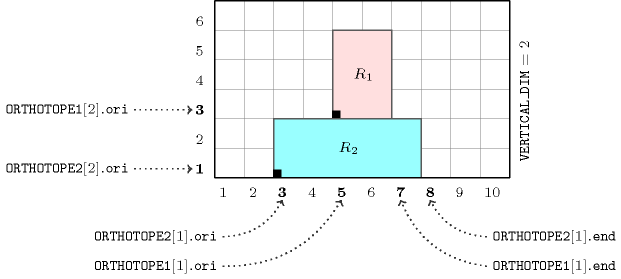
As illustrated by Figure 5.312.1 the orthotope $𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1$ (rectangle R1 coloured in pink) is on top of $𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 2$ (rectangle R2 coloured in blue) according to the hypothesis that the vertical dimension corresponds to dimension 2 (i.e., $𝚅𝙴𝚁𝚃𝙸𝙲𝙰𝙻_𝙳𝙸𝙼 = 2$ ). This stands from the fact that the following conditions hold:

$𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 2 [2] . 𝚘𝚛𝚒 + 𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 2 [2] . 𝚜𝚒𝚣 = 1 + 2 = 𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1 [2] . 𝚘𝚛𝚒$ ,
$𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 2 [1] . 𝚘𝚛𝚒 = 3 \leq 𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1 [1] . 𝚘𝚛𝚒 = 5$ ,
$𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1 [1] . 𝚎𝚗𝚍 = 7 \leq 𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 2 [1] . 𝚎𝚗𝚍 = 8$ .

Consequently, the $𝚘𝚛𝚝𝚑_𝚘𝚗_𝚝𝚘𝚙_𝚘𝚏_𝚘𝚛𝚝𝚑$ constraint holds.

Figure 5.312.1. Illustration of the relation on top of of the Example slot ( $R_{1}$ on top of $R_{2}$ wrt dimension $𝚅𝙴𝚁𝚃𝙸𝙲𝙰𝙻_𝙳𝙸𝙼 = 2$ )

Typical

| 𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 | > 1

𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 . 𝚜𝚒𝚣 > 0

Used in

$𝚙𝚕𝚊𝚌𝚎_𝚒𝚗_𝚙𝚢𝚛𝚊𝚖𝚒𝚍$ .

Keywords

constraint type: logic.

geometry: geometrical constraint, non-overlapping, orthotope.

Arc input(s)

$𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1$ $𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 2$

Arc generator

𝑃𝑅𝑂𝐷𝑈𝐶𝑇

(=) \mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 1, 𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 2)

Arc arity

Arc constraint(s)

• 𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 1 . 𝚔𝚎𝚢 \neq 𝚅𝙴𝚁𝚃𝙸𝙲𝙰𝙻_𝙳𝙸𝙼

• 𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 2 . 𝚘𝚛𝚒 \leq 𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 1 . 𝚘𝚛𝚒

• 𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 1 . 𝚎𝚗𝚍 \leq 𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 2 . 𝚎𝚗𝚍

Graph property(ies)

𝐍𝐀𝐑𝐂

= | 𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1 | - 1

Arc input(s)

$𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1$ $𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 2$

Arc generator

𝑃𝑅𝑂𝐷𝑈𝐶𝑇

(=) \mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 1, 𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 2)

Arc arity

Arc constraint(s)

• 𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 1 . 𝚔𝚎𝚢 = 𝚅𝙴𝚁𝚃𝙸𝙲𝙰𝙻_𝙳𝙸𝙼

• 𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 1 . 𝚘𝚛𝚒 = 𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 2 . 𝚎𝚗𝚍

Graph property(ies)

𝐍𝐀𝐑𝐂

= 1

Graph model

The first and second graph constraints respectively express the first and second conditions stated in the Purpose slot defining the $𝚘𝚛𝚝𝚑_𝚘𝚗_𝚝𝚘𝚙_𝚘𝚏_𝚘𝚛𝚝𝚑$ constraint.

Parts (A) and (B) of Figure 5.312.2 respectively show the initial and final graph associated with the second graph constraint of the Example slot. Since we use the $𝐍𝐀𝐑𝐂$ graph property, the unique arc of the final graph is stressed in bold.

Figure 5.312.2. Initial and final graph of the $𝚘𝚛𝚝𝚑_𝚘𝚗_𝚝𝚘𝚙_𝚘𝚏_𝚘𝚛𝚝𝚑$ constraint


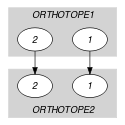
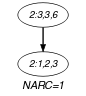
(a)	(b)

Signature

Consider the second graph constraint. Since all the $𝚔𝚎𝚢$ attributes of the $𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1$ collection are distinct, because of the arc constraint $𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 1 . 𝚔𝚎𝚢 = 𝚅𝙴𝚁𝚃𝙸𝙲𝙰𝙻_𝙳𝙸𝙼$ , and since we use the $𝑃𝑅𝑂𝐷𝑈𝐶𝑇 (=)$ arc generator the final graph contains at most one arc. Therefore we can rewrite the graph property $𝐍𝐀𝐑𝐂 = 1$ to $𝐍𝐀𝐑𝐂 \geq 1$ and simplify $\underset{̲}{\bar{𝐍𝐀𝐑𝐂}}$ to $\bar{𝐍𝐀𝐑𝐂}$ .

Global Constraint Catalog

5. Global Constraint Catalogue

5.312. orth_on_top_of_orth

Figure 5.312.1. Illustration of the relation on top of of the Example slot (R 1 on top of R 2 wrt dimension 𝚅𝙴𝚁𝚃𝙸𝙲𝙰𝙻_𝙳𝙸𝙼=2)

Figure 5.312.2. Initial and final graph of the 𝚘𝚛𝚝𝚑_𝚘𝚗_𝚝𝚘𝚙_𝚘𝚏_𝚘𝚛𝚝𝚑 constraint

Figure 5.312.1. Illustration of the relation on top of of the Example slot ( $R_{1}$ on top of $R_{2}$ wrt dimension $𝚅𝙴𝚁𝚃𝙸𝙲𝙰𝙻_𝙳𝙸𝙼 = 2$ )

Figure 5.312.2. Initial and final graph of the $𝚘𝚛𝚝𝚑_𝚘𝚗_𝚝𝚘𝚙_𝚘𝚏_𝚘𝚛𝚝𝚑$ constraint