Global Constraint Catalog: Ctwo_orth

5.411. two_orth_include

DESCRIPTION

LINKS

GRAPH

Origin

Used for defining $𝚍𝚒𝚏𝚏𝚗_𝚒𝚗𝚌𝚕𝚞𝚍𝚎$ .

Constraint

$𝚝𝚠𝚘_𝚘𝚛𝚝𝚑_𝚒𝚗𝚌𝚕𝚞𝚍𝚎 (𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1, 𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 2, 𝙳𝙸𝙼)$

Type

𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴

𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚘𝚛𝚒 - 𝚍𝚟𝚊𝚛, 𝚜𝚒𝚣 - 𝚍𝚟𝚊𝚛, 𝚎𝚗𝚍 - 𝚍𝚟𝚊𝚛)

Arguments

$𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1$	$𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴$
$𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 2$	$𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴$
$𝙳𝙸𝙼$	$𝚒𝚗𝚝$

Restrictions

| 𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 | > 0

𝚛𝚎𝚚𝚞𝚒𝚛𝚎_𝚊𝚝_𝚕𝚎𝚊𝚜𝚝

(2, 𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴, [𝚘𝚛𝚒, 𝚜𝚒𝚣, 𝚎𝚗𝚍])

𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 . 𝚜𝚒𝚣 \geq 0

𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 . 𝚘𝚛𝚒 \leq 𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 . 𝚎𝚗𝚍

| 𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1 | = | 𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 2 |

𝚘𝚛𝚝𝚑_𝚕𝚒𝚗𝚔_𝚘𝚛𝚒_𝚜𝚒𝚣_𝚎𝚗𝚍

(𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1)

𝚘𝚛𝚝𝚑_𝚕𝚒𝚗𝚔_𝚘𝚛𝚒_𝚜𝚒𝚣_𝚎𝚗𝚍

(𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 2)

𝙳𝙸𝙼 > 0

𝙳𝙸𝙼 \leq | 𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1 |

Purpose

Let $P_{1}$ and $P_{2}$ respectively denote the projections of $𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1$ and $𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 2$ onto dimension $𝙳𝙸𝙼$ . If $P_{1}$ and $P_{2}$ overlap then, either $P_{1}$ is included in $P_{2}$ , either $P_{2}$ is included in $P_{1}$ .

Example

(\begin{matrix} 〈𝚘𝚛𝚒 - 1 𝚜𝚒𝚣 - 3 𝚎𝚗𝚍 - 4, 𝚘𝚛𝚒 - 1 𝚜𝚒𝚣 - 1 𝚎𝚗𝚍 - 2〉, \\ 〈𝚘𝚛𝚒 - 1 𝚜𝚒𝚣 - 2 𝚎𝚗𝚍 - 3, 𝚘𝚛𝚒 - 2 𝚜𝚒𝚣 - 3 𝚎𝚗𝚍 - 5〉, 1 \end{matrix})

Figure 5.411.1. Initial and final graph of the $𝚝𝚠𝚘_𝚘𝚛𝚝𝚑_𝚒𝚗𝚌𝚕𝚞𝚍𝚎$ constraint


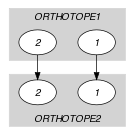
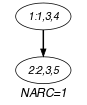
(a)	(b)

Typical

| 𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 | > 1

Symmetry

Arguments are permutable w.r.t. permutation $(𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1, 𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 2)$ $(𝙳𝙸𝙼)$ .

Used in

$𝚍𝚒𝚏𝚏𝚗_𝚒𝚗𝚌𝚕𝚞𝚍𝚎$ .

See also

implied by: $𝚝𝚠𝚘_𝚘𝚛𝚝𝚑_𝚌𝚘𝚕𝚞𝚖𝚗$ .

related: $𝚍𝚒𝚏𝚏𝚗$ (an extension of the $𝚍𝚒𝚏𝚏𝚗$ constraint).

Keywords

constraint type: logic.

geometry: geometrical constraint, positioning constraint, orthotope.

Arc input(s): $𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 1$ $𝙾𝚁𝚃𝙷𝙾𝚃𝙾𝙿𝙴 2$
Arc generator: $𝑃𝑅𝑂𝐷𝑈𝐶𝑇$ $(=) \mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 1, 𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 2)$
Arc arity
Arc constraint(s): $\begin{matrix} ⋀ (\begin{matrix} 𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 1 . 𝚔𝚎𝚢 = 𝙳𝙸𝙼, \\ 𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 1 . 𝚘𝚛𝚒 < 𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 2 . 𝚎𝚗𝚍, \\ 𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 2 . 𝚘𝚛𝚒 < 𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 1 . 𝚎𝚗𝚍, \\ 𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 1 . 𝚜𝚒𝚣 > 0, \\ 𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 2 . 𝚜𝚒𝚣 > 0 \end{matrix}) \Rightarrow \\ \begin{matrix} \begin{matrix} 𝚖𝚒𝚗 (𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 1 . 𝚎𝚗𝚍, 𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 2 . 𝚎𝚗𝚍) - \\ 𝚖𝚊𝚡 (𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 1 . 𝚘𝚛𝚒, 𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 2 . 𝚘𝚛𝚒) \end{matrix} = \\ 𝚖𝚒𝚗 (𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 1 . 𝚜𝚒𝚣, 𝚘𝚛𝚝𝚑𝚘𝚝𝚘𝚙𝚎 2 . 𝚜𝚒𝚣) \end{matrix} \end{matrix}$
Graph property(ies): $𝐍𝐀𝐑𝐂$ $= 1$

Global Constraint Catalog

5. Global Constraint Catalogue

5.411. two_orth_include

Figure 5.411.1. Initial and final graph of the 𝚝𝚠𝚘_𝚘𝚛𝚝𝚑_𝚒𝚗𝚌𝚕𝚞𝚍𝚎 constraint

Figure 5.411.1. Initial and final graph of the $𝚝𝚠𝚘_𝚘𝚛𝚝𝚑_𝚒𝚗𝚌𝚕𝚞𝚍𝚎$ constraint