5.323. place_in_pyramid
| DESCRIPTION | LINKS | GRAPH |
- Origin
N. Beldiceanu
- Constraint
- Type
- Arguments
- Restrictions
- Purpose
For each pair of orthotopes of the collection , and do not overlap (two orthotopes do not overlap if there exists at least one dimension where their projections do not overlap). In addition, each orthotope of the collection should be supported by one other orthotope or by the ground. The vertical dimension is given by the parameter .
- Example
-
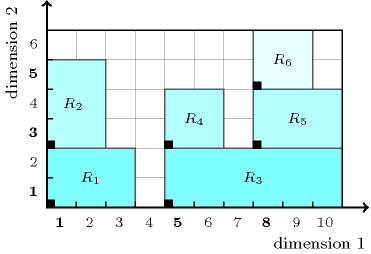
Figure 5.323.1 depicts the placement associated with the example, where the item of the collection is represented by the rectangle Ri. The constraint holds since the rectangles do not overlap and since rectangles R1, R2, R3, R4, R5, and R6 are respectively supported by the ground, R1, the ground, R3, R3, and R5.
Figure 5.323.1. Solution corresponding to the Example slot
- Typical
- Symmetry
Items of are permutable.
- Usage
The constraint is not enough if one wants to produce a placement where no orthotope floats in the air. This constraint is usually handled with a heuristic during the enumeration phase.
- See also
- Keywords
-
geometry: geometrical constraint, non-overlapping, orthotope.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
The arc constraint of the graph constraint forces one of the following conditions:
If the arc connects the same orthotope then the ground directly supports ,
Otherwise, if we have an arc from an orthotope to a distinct orthotope , the condition is: is on top of (i.e., in all dimensions, except dimension , the projection of is included in the projection of , while in dimension the projection of is located after the projection of ).
Parts (A) and (B) of Figure 5.323.2 respectively show the initial and final graph associated with the Example slot. Since we use the graph property, the arcs of the final graph are stressed in bold.
Figure 5.323.2. Initial and final graph of the constraint
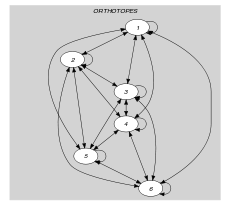
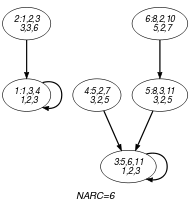
(a) (b)