5.35. assign_and_nvalues
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
Given several items (each of them having a specific value that may not be initially fixed), and different bins, assign each item to a bin, so that the number of distinct values in each bin satisfies the condition .
- Example
-
Figure 5.35.1 depicts the solution corresponding to the example.
Figure 5.35.1. An assignment with at most two distinct values in parallel (values 3 and 4 in bin 2 and value 5 in bin 1)
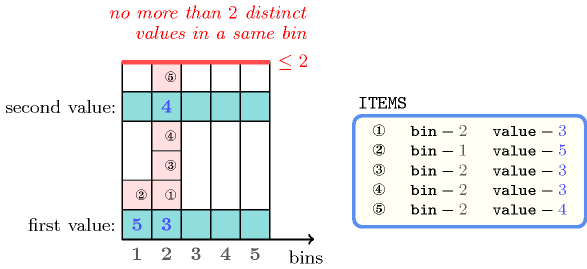
The constraint holds since for each used bin (i.e., namely bins 1 and 2) the number of distinct colours of the corresponding assigned items is less than or equal to the limit 2.
- Typical
- Symmetries
Items of are permutable.
All occurrences of two distinct values of can be swapped; all occurrences of a value of can be renamed to any unused value.
- Arg. properties
Contractible wrt. when .
Extensible wrt. when .
- Usage
Let us give two examples where the constraint is useful:
Quite often, in bin-packing problems, each item has a specific type, and one wants to assign items of similar type to each bin.
In a vehicle routing problem, one wants to restrict the number of towns visited by each vehicle. Note that several customers may be located at the same town. In this example, each bin would correspond to a vehicle, each item would correspond to a visit to a customer, and the colour of an item would be the location of the corresponding customer.
- See also
assignment dimension removed: , .
common keyword: (number of distinct values).
related: .
- Keywords
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph class
-
- Sets
-
- Constraint(s) on sets
- Graph model
We enforce the constraint on the items that are assigned to the same bin.
Parts (A) and (B) of Figure 5.35.2 respectively show the initial and final graph associated with the Example slot. The final graph consists of the following two connected components:
The connected component containing 8 vertices corresponds to the items that are assigned to bin 2.
The connected component containing 2 vertices corresponds to the items that are assigned to bin 1.
Figure 5.35.2. Initial and final graph of the constraint
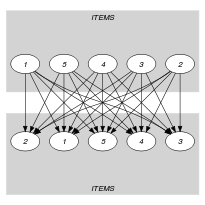
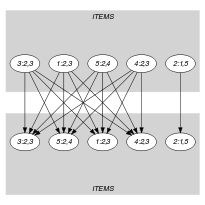
(a) (b) The constraint holds since for each set of successors of the vertices of the final graph no more than two distinct values are used:
The unique item assigned to bin 1 uses value 5.
Items assigned to bin 2 use values 3 and 4.