Generalisation of $\mathrm{𝚍𝚒𝚏𝚏𝚗}$.

$\mathrm{𝚐𝚎𝚘𝚜𝚝}\_\mathrm{𝚝𝚒𝚖𝚎}(𝙺,\mathrm{𝙳𝙸𝙼𝚂},\mathrm{𝙾𝙱𝙹𝙴𝙲𝚃𝚂},\mathrm{𝚂𝙱𝙾𝚇𝙴𝚂})$

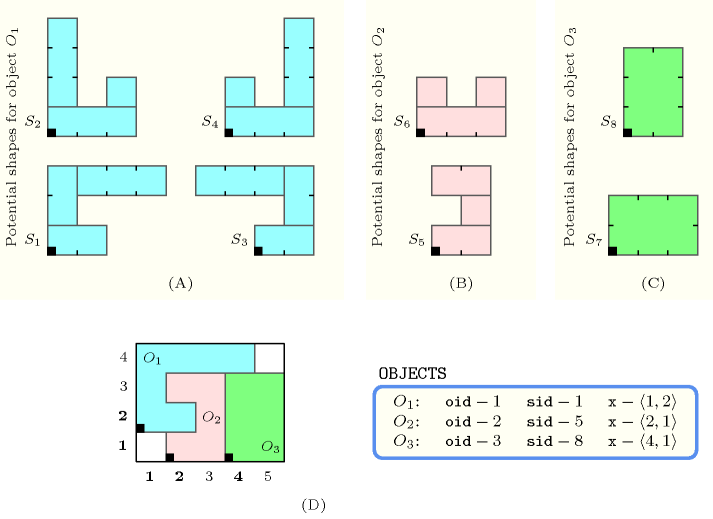
Parts (A), (B) and (C) of Figure 5.160.1 respectively represent the potential shapes associated with the three objects of the example. Part (D) shows the position of the three objects of the example, where the first, second and third objects were respectively assigned shapes 1, 5 and 8. The coordinates of the leftmost lowest corner of each object are stressed in bold. The $\mathrm{𝚐𝚎𝚘𝚜𝚝}\_\mathrm{𝚝𝚒𝚖𝚎}$ constraint holds since the three objects do not overlap: even though the time intervals associated with each object overlap (i.e., they are in fact identical), their corresponding shapes do not overlap (i.e., see part (D) if Figure 5.160.1).

Figure 5.160.1. (D) The three non-overlapping objects $O_1$, $O_2$, $O_3$ of the Example slot respectively assigned shapes $S_1$, $S_5$, $S_8$; (A), (B), (C) shapes $S_1$, $S_2$, $S_3$, $S_4$, $S_5$, $S_6$, $S_7$ and $S_8$ are respectively made up from 3, 3, 3, 3, 3, 3, 1 and 1 disjoint shifted box.

• Items of $\mathrm{𝙾𝙱𝙹𝙴𝙲𝚃𝚂}$ are permutable.

• Items of $\mathrm{𝚂𝙱𝙾𝚇𝙴𝚂}$ are permutable.

• Items of $\mathrm{𝙾𝙱𝙹𝙴𝙲𝚃𝚂}.𝚡$, $\mathrm{𝚂𝙱𝙾𝚇𝙴𝚂}.𝚝$ and $\mathrm{𝚂𝙱𝙾𝚇𝙴𝚂}.𝚕$ are permutable (same permutation used).

• $\mathrm{𝚂𝙱𝙾𝚇𝙴𝚂}.𝚕.𝚟$ can be decreased to any value $\ge 1$.

• One and the same constant can be added to the $\mathrm{𝚜𝚝𝚊𝚛𝚝}$ and $\mathrm{𝚎𝚗𝚍}$ attributes of all items of $\mathrm{𝙾𝙱𝙹𝙴𝙲𝚃𝚂}$.

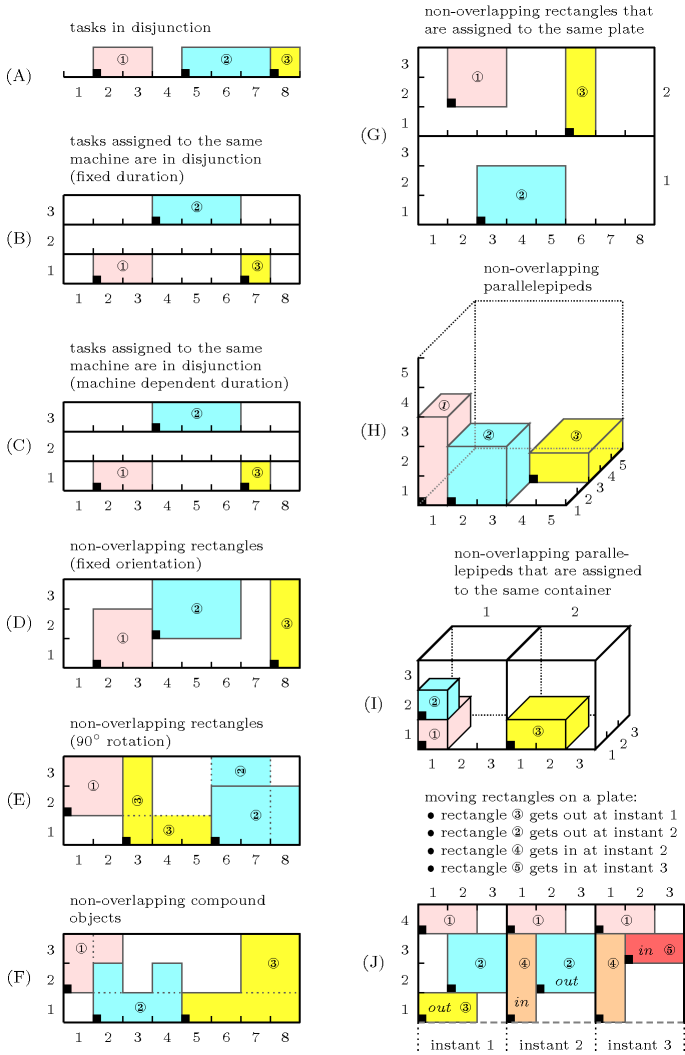
The $\mathrm{𝚐𝚎𝚘𝚜𝚝}\_\mathrm{𝚝𝚒𝚖𝚎}$ constraint allows to model directly a large number of placement problems. Figure 5.160.2 sketches ten typical use of the $\mathrm{𝚐𝚎𝚘𝚜𝚝}\_\mathrm{𝚝𝚒𝚖𝚎}$ constraint:

• The first case (A) corresponds to a non-overlapping constraint among three segments (or three tasks in disjunction).

• The second, third and fourth cases (B,C,D) correspond to a non-overlapping constraint between rectangles where (B) and (C) are special cases where the sizes of all rectangles in the second dimension are equal to 1; this can be interpreted as a machine assignment problem where each rectangle corresponds to a non-pre-emptive task that has to be placed in time and assigned to a specific machine so that no two tasks assigned to the same machine overlap in time. In Part (B) the duration of each task is fixed, while in Part (C) the duration depends on the machine to which the task is actually assigned. This dependence can be expressed by the $\mathrm{𝚎𝚕𝚎𝚖𝚎𝚗𝚝}$ constraint, which specifies the dependence between the shape variable and the assignment variable of each task.

• The fifth case (E) corresponds to a non-overlapping constraint between rectangles where each rectangle can have two orientations. This is achieved by associating with each rectangle two shapes of respective sizes $l·h$ and $h·l$. Since their orientation is not initially fixed, an $\mathrm{𝚎𝚕𝚎𝚖𝚎𝚗𝚝}\_\mathrm{𝚕𝚎𝚜𝚜𝚎𝚚}$ constraint can be used for enforcing the three rectangles to be included within the bounding box defined by the origin's coordinates $1,1$ and sizes $8,3$.

• The sixth case (F) corresponds to a non-overlapping constraint between more complex objects where each object is described by a given set of rectangles.

• The seventh case (G) describes a rectangle placement problem where one has to first assign each rectangle to a strip so that all rectangles that are assigned to the same strip do not overlap.

• The eighth case (H) corresponds to a non-overlapping constraint between parallelepipeds.

• The ninth case (I) can be interpreted as a non-overlapping constraint between parallelepipeds that are assigned to the same  container. The first dimension corresponds to the identifier of the  container, while the next three dimensions are associated with the position of a parallelepiped inside a  container.

• Finally the tenth case (J) describes a rectangle placement problem over three consecutive time-slots: rectangles assigned to the same time-slot should not overlap in time. We initially start with the three rectangles 1, 2 and 3. Rectangle 3 is no more present at instant 2 (the arrow $\downarrow$ within rectangle 3 at time 1 indicates that rectangle 3 will disappear at the next time-point), while rectangle 4 appears at instant 2 (the arrow $\uparrow$ within rectangle 4 at time 2 denotes the fact that the rectangle 4 appears at instant 2). Finally rectangle 2 disappears at instant 3 and is replaced by rectangle 5.

Figure 5.160.2. Ten typical examples of use of the $\mathrm{𝚐𝚎𝚘𝚜𝚝}\_\mathrm{𝚝𝚒𝚖𝚎}$ constraint (ground instances)

A sweep-based filtering algorithm for this constraint is described in [BeldiceanuCarlssonPoderSadekTruchet07]. Unlike previous sweep filtering algorithms which move a line for finding a feasible position for the origin of an object, this algorithm performs a recursive traversal of the multidimensional placement space. It explores all points of the domain of the origin of the object under focus, one by one, in increasing lexicographic order, until a point is found that is not infeasible for any non-overlapping constraints. To make the search efficient, instead of moving each time to the successor point, the search is arranged so that it skips points that are known to be infeasible for some non-overlapping constraint.

geost in Choco, geost in JaCoP.

common keyword: $\mathrm{𝚍𝚒𝚏𝚏𝚗}$, $\mathrm{𝚗𝚘𝚗}\_\mathrm{𝚘𝚟𝚎𝚛𝚕𝚊𝚙}\_\mathrm{𝚜𝚋𝚘𝚡𝚎𝚜}$ (geometrical constraint,non-overlapping), $\mathrm{𝚟𝚒𝚜𝚒𝚋𝚕𝚎}$ (geometrical constraint,sweep).

specialisation: $\mathrm{𝚐𝚎𝚘𝚜𝚝}$ ($\mathrm{𝚝𝚎𝚖𝚙𝚘𝚛𝚊𝚕}$ $\mathrm{𝚍𝚒𝚖𝚎𝚗𝚜𝚒𝚘𝚗}$ removed).

constraint type: decomposition, timetabling constraint, predefined constraint.

filtering: sweep.

geometry: geometrical constraint, non-overlapping.

modelling: assignment dimension, assignment to the same set of values, assigning and scheduling tasks that run in parallel, disjunction.

modelling exercises: assignment to the same set of values, assigning and scheduling tasks that run in parallel.