3.7.182. Partridge

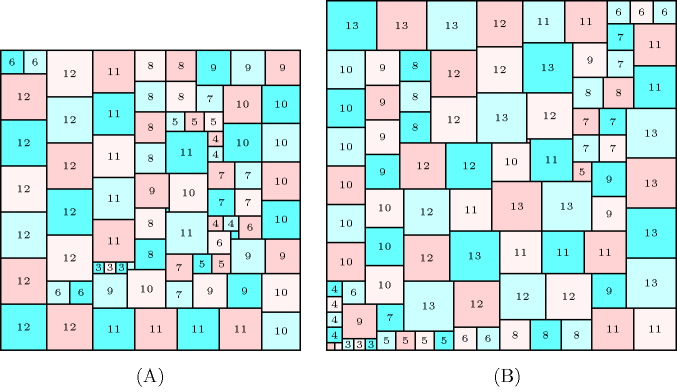
Denotes that a constraint can be used for solving the Partridge problem: the Partridge problem consists of tiling a square of size n·(n+1) 2 by n·(n+1) 2 squares of respective size

  • 1 square of size 1,

  • 2 squares of size 2,

  •  ⋯ ,

  • n squares of size n.

It was initially proposed by R. Wainwright and is based on the identity 1·1 2 +2·2 2 +⋯+n·n 2 =(n·(n+1) 2) 2 . The problem is described in http://mathpuzzle.com/partridge.html. Part (A) of Figure 3.7.49 gives a solution for n=12 found with 𝚐𝚎𝚘𝚜𝚝 [AgrenCarlssonBeldiceanuSbihiTruchetZampelli09a], while Part (B) provides a solution for n=13 found by S. Hougardy [Hougardy12].

Figure 3.7.49. (A) a solution to the Partridge problem for n=12, and (B) a solution for n=13
ctrs/preface-189-tikz