Consider a conjunction $𝒞$ of constraints such that:

1. The constraint network $𝒩$ corresponding to the conjunction $𝒞$ is not Berge-acyclic.

2. The filtering algorithms associated with the different constraints of the conjunction $𝒞$ all achieve arc-consistency.

In this context, one can design a heuristics that fix enough variables, but not all, so that the remaining constraint network $𝒩$ becomes Berge-acyclic.The point is that, as soon as the constraint network becomes Berge-acyclic no search is needed any more to check that there is a solution, provided we achieve arc-consistency on the remaining constraints. This stems from [DechterPearl88], which itself is a consequence of [Freuder82]. This can be achieved by fixing the variables in such a way that some constraints get entailed even though they still mention some variables that are not yet fixed. Let us illustrate that idea on a matrix model where we have a $R\times K$ matrix $ℳ$ of domain variables taking a value in interval $[1,V]$. Assume that:

• On each row of $ℳ$ we have a constraint that can be described in term of a counter-free automaton.

• On each column of $ℳ$ we have a $\mathrm{𝚐𝚕𝚘𝚋𝚊𝚕}\_\mathrm{𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢}\_\mathrm{𝚕𝚘𝚠}\_\mathrm{𝚞𝚙}$ constraint that only imposes a minimum number of occurrences for each value in $[1,V]$ (i.e., the maximum number of occurrences is not constrained at all).

Note that arc-consistency can be achieved for such constraints. For this constraint pattern, an assignment strategy that systematically tries creating a Berge-acyclic constraint network can be achieved as follows. Fix some variables so that $K-1$ column constraints (i.e., $\mathrm{𝚐𝚕𝚘𝚋𝚊𝚕}\_\mathrm{𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢}\_\mathrm{𝚕𝚘𝚠}\_\mathrm{𝚞𝚙}$ constraints) get entailed. If this is the case the remaining constraint network consists of $R$ rows constraints and of a single column constraint.

Figure 3.7.34. (A) Initial constraint network for a $R=3$ by $K=4$ matrix (with column constraints $C_1$, $C_2$, $C_3$, $C_4$ and row constraints $C_5$, $C_6$, $C_7$) and (B) corresponding intersection graph; (C) Berge-acyclic constraint network after the entailment of the column constraints $C_2$, $C_3$ and $C_4$ and (D) corresponding cycle-free intersection graph.

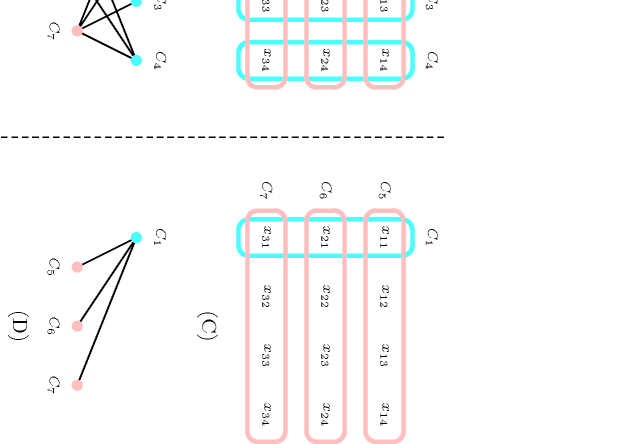
As illustrated by Figure 3.7.34, this typically corresponds to a Berge-acyclic constraint network. Let us now finally explain how to assign values to a subset of variables of a $\mathrm{𝚐𝚕𝚘𝚋𝚊𝚕}\_\mathrm{𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢}\_\mathrm{𝚕𝚘𝚠}\_\mathrm{𝚞𝚙}$ constraint that only restricts the minimum number of occurrences of certain values so that it becomes entailed. As an example, let us consider a $\mathrm{𝚐𝚕𝚘𝚋𝚊𝚕}\_\mathrm{𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢}\_\mathrm{𝚕𝚘𝚠}\_\mathrm{𝚞𝚙}$ constraint involving 10 variables which forces at least three occurrences of value 1 and one occurrence of value 2. A heuristics needs only fixing 4 variables out of the 10 variables to values 1, 1, 1 and 2 so that the corresponding $\mathrm{𝚐𝚕𝚘𝚋𝚊𝚕}\_\mathrm{𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢}\_\mathrm{𝚕𝚘𝚠}\_\mathrm{𝚞𝚙}$ gets entailed. A typical instance of this pattern corresponds to nurse scheduling problems where:

• Each row of $ℳ$ corresponds to the timetable of a person over $K$ consecutive days. Using a counter free automaton the corresponding row constraint encodes all legal rules of a valid schedule.

• Each column of $ℳ$ describes the request for a minimum number of services on a given day. Types of work (i.e., values in $[1,V]$) can for instance be interpreted as a morning shift, an afternoon shift, a night shift or a day off.

The heuristics first addresses the coverage constraints only (i.e., the $\mathrm{𝚐𝚕𝚘𝚋𝚊𝚕}\_\mathrm{𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢}\_\mathrm{𝚕𝚘𝚠}\_\mathrm{𝚞𝚙}$ constraints). It seeks to assign enough nurses to given shifts on given day to satisfy all but one coverage constraints. Once this is done, the remaining variables can be labelled without search.