3.7.49. Compulsory part
A constraint for which the filtering algorithm may use the notion of compulsory part. The notion of compulsory part was introduced by A. Lahrichi within the context of cumulative scheduling problems [Lahrichi79], [Lahrichi82], [Lahrichi82a] as well as within the context of rectangles placement problems [LahrichiGondran84]. Within these two contexts, the compulsory part respectively corresponds to the intersection of all feasible instances of a task or to the intersection of all feasible instances of a rectangle.
Figure 3.7.13. Illustration of the notion of compulsory part
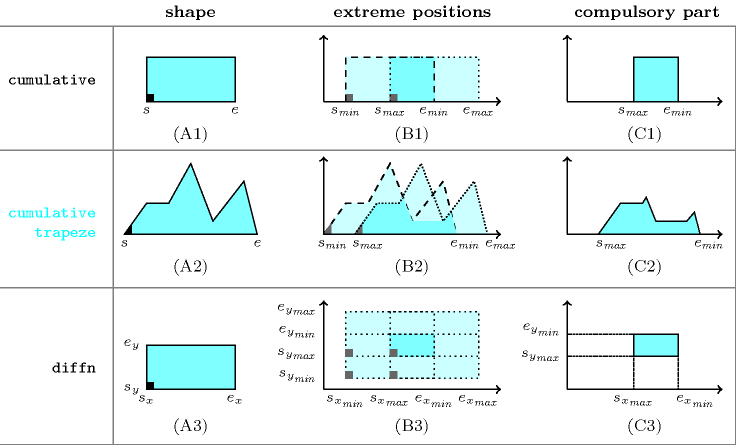
Figure 3.7.13 illustrates the notion of compulsory part in the context of scheduling and placement problems. The first, second and third rows respectively corresponds to the [AggounBeldiceanu93], the [Poder02], [PoderBeldiceanuSanlaville04] and the [BeldiceanuGuoThiel01] constraints. The first, second and third columns respectively correspond to the shape of the object for which we compute the compulsory part, to the extreme positions of the object and to the corresponding compulsory part. When both, the shape of an object is convex and the domain of its origin is also convex, we do not need to consider all feasible instances of the object to compute its compulsory part. We only need to position the object to the extreme positions of its domain and to compute the intersection to get its compulsory part [BeldiceanuGuoThiel01].
This is the case of the constraint where a task is positioned to its earliest and latest starts and (see the first row and second column of Figure 3.7.13).
This is also the case of the constraint where an orthotope is positioned to its extreme positions, where is the number of dimensions of the placement space (see the third row and second column of Figure 3.7.13, where the origin of the rectangle is fixed to the extreme positions , , , and ).
But this is not the case of the constraint with a task that has a valley, i.e. a task for which a resource consumption decrease is followed by a resource consumption increase. In addition of computing the intersection between the two extreme positions and of a task, we must also consider the valleys to further reduce as explained now [PoderBeldiceanuSanlaville04]. The end of a valley is the lowest rightmost point of a valley. We must remove from all parts that are located both (1) between the earliest start and latest end of the valley end, (2) and on top of the valley. Figure 3.7.14 illustrates this point for the task used in the second row and first column of Figure 3.7.13.
Figure 3.7.14. Illustrating the computation of the compulsory part of a task with a valley: (A) the task shape and its valley end in red, (B) in cyan the intersection between the task positioned at its earliest start (in dashed) and its latest start (in dotted); in pink the part located (1) between the earliest and latest positions of the valley end, and (2) on top of the valley, (C) the compulsory part of the task, i.e., from which we remove the pink part on top of the valley.