3.7.212. Relaxation dimension
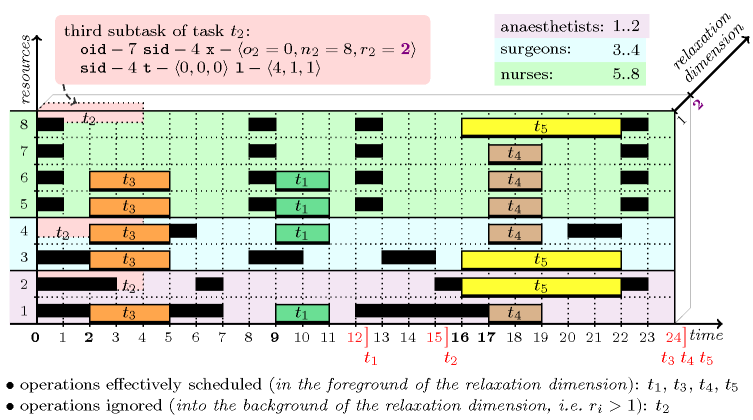
modelling: relaxation dimension A constraint that allows the modelling of constraint relaxation in the context of placement problems. This is achieved by adding an extra dimension to the placement space where objects that are really considered are in the foreground, while objects that are discarded are rejected into the background. As a concrete example, consider a slight modification of the data of the task assignment and scheduling problem that is described at the keyword entry assigning and scheduling tasks that run in parallel. In this problem the four nurses are all not available during the time periods , , and . We now rather consider the following unavailability periods , , and . Under this new hypothesis we cannot anymore schedule all the five surgery tasks , , , and , i.e., we get a no solution answer if we use the model described in assigning and scheduling tasks that run in parallel. In this model we are using a two-dimensional constraint, where the first and second dimensions respectively correspond to the time and resource axes. Now, in order to permit relaxation, we introduce a third dimension, a relaxation dimension. The idea is to map each task to a parallelepiped for which the size in the relaxation dimension is equal to one. In addition, the coordinate of a parallelepiped in the relaxation dimension is a variable taking its value in the interval , where represents the number of operations to schedule (i.e., for each surgery task we create a coordinate variable where stands for relaxation. Then, all parallelepipeds for which the coordinate in the relaxation dimension is set to 1 correspond to surgery tasks that are effectively scheduled, while all other parallelepipeds represent surgery tasks that are discarded. On the one hand, this model allows the direct expression of relaxation right from the beginning without introducing any extra soft constraint and without dynamically adding any constraint during search. On the other hand, a disadvantage is that the model does not directly consider an optimisation criterion like, for instance, the maximum number of tasks effectively scheduled, or the sum of the durations of the tasks effectively done; this can be modelled using extra constraints but this does not provide sharp bounds on the optimisation criterion. Nevertheless, this gives a compact model, especially in the context where additional constraints complicate the computation of a sharp bound. Going back to the example described at the keyword entry assigning and scheduling tasks that run in parallel, we get the following three-dimensional constraint:
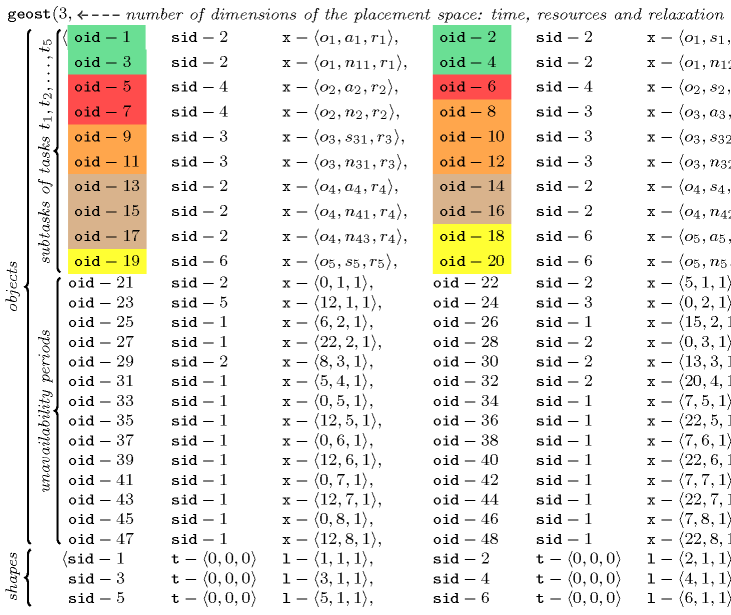
Figure 3.7.56 depicts a solution to the problem corresponding to the assignment
During search, the relaxation variables , , , , are first set to value one (i.e., the corresponding operations are scheduled) and then, upon backtracking, assigned to any value greater than one (i.e., there is no backtrack on the values that are greater than one since we just want to reject an operation into the background).
Figure 3.7.56. A partial solution to the surgery scheduling problem that maximises the number of operations actually performed where only operation is not scheduled