• $\mathrm{𝚌𝚊𝚕𝚎𝚗𝚍𝚊𝚛}$,

• $\mathrm{𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎𝚜}$,

• $\mathrm{𝚍𝚒𝚏𝚏𝚗}$,

• $\mathrm{𝚐𝚎𝚘𝚜𝚝}$.

modelling: scheduling with machine choice, calendars and preemption A set of constraints that can be used for modelling a scheduling problem where:

• We have tasks that have both to be assigned to machine and time.

• Each task has a fixed duration.

• Machines can run at most one task at a given instant.

• Each machine has its own fixed unavailability periods (i.e., a calendar of unavailability periods).

• An unavailability period that allows (respectively forbids) a task to be interrupted and resumed just after is called crossable (respectively non-crossable). A task that can be (respectively cannot be) interrupted by a crossable unavailability period is called resumable (respectively non-resumable).

• We have a precedence constraint between specific pairs of tasks. Each precedence forces that a given task ends before the start of another given task.

This model illustrates the use of two time coordinates systems:

• The first coordinate system, so called the virtual coordinate system, does not consider at all the crossable unavailability periods associated with the different machines. Since resumable tasks can be preempted by machine crossable unavailability, all resource scheduling constraints (i.e., $\mathrm{𝚍𝚒𝚏𝚏𝚗}$, $\mathrm{𝚐𝚎𝚘𝚜𝚝}$) are expressed within this first coordinate system. This stands from the fact that resource scheduling constraints like $\mathrm{𝚍𝚒𝚏𝚏𝚗}$ or $\mathrm{𝚐𝚎𝚘𝚜𝚝}$ do not support preemption.

• The second coordinate system, so called the real coordinate system, considers all timepoints whether they correspond or not to crossable unavailability periods. All temporal constraints (i.e., precedence constraints represented by $\mathrm{𝚕𝚎𝚚}$ constraints in this model) are expressed with respect to this second coordinate system.

Consequently, each task has a start and an end that are expressed within the virtual coordinate system as well as within the real coordinate system.

• Each task, whether it is resumable or not, is passed to the resource scheduling constraints as well as to the precedence constraints. In addition, we represent each non-crossable unavailability period as a fixed task that is also passed to the resource scheduling constraints.

• The $\mathrm{𝚌𝚊𝚕𝚎𝚗𝚍𝚊𝚛}$ constraint ensures the link between variables (i.e., the start and the end of the tasks no matter whether they are resumable or not) expressed in these two coordinate systems with respect to the crossable unavailability periods.

We now provide the corresponding detailed model. Given:

1. A set of machines $ℳ=\{m_1,m_2,\cdots ,m_p\}$, where each machine has a list of fixed unavailability periods. An unavailability $u_i$ is defined by the following attributes:

   1. The crossable flag $c_i$ tells whether unavailability $u_i$ is crossable ($c_i=1$) or not ($c_i=0$).

   2. The machine $r_i$ indicates the machine (i.e., a value in $[1,p]$) to which unavailability $u_i$ corresponds (i.e., since different machines may have different unavailability periods).

   3. The start $s_i$ of the unavailability $u_i$ which indicates the first unavailable timepoint of the unavailability.

   4. The end $e_i$ of the unavailability $u_i$ which gives the last unavailable timepoint of the unavailability.

2. A set of tasks $𝒯=\{t_1,t_2,\cdots ,t_n\}$, where each task $t_i$ (with $i\in [1,n]$) has the following attributes which are all domain variables except the resumable flag and the virtual duration:

   1. The resumable flag $r_i$ tells whether task $t_i$ is resumable ($r_i=1$) or not ($r_i=0$).

   2. The machine $m_i$ indicates the machine (i.e., a value in $[1,p]$) to which task $t_i$ will be assigned.

   3. The virtual start ${\mathrm{𝑣𝑠}}_i$ gives the start of task $t_i$ in the virtual coordinate system.

   4. The virtual duration ${\mathrm{𝑣𝑑}}_i$ corresponds to the duration of task $t_i$ without counting the eventual unavailability periods crossed by task $t_i$.

   5. The virtual end ${\mathrm{𝑣𝑒}}_i$ provides the end of task $t_i$ in the virtual coordinate system. We have that ${\mathrm{𝑣𝑠}}_i+{\mathrm{𝑣𝑑}}_i={\mathrm{𝑣𝑒}}_i$.

   6. The real start ${\mathrm{𝑟𝑠}}_i$ gives the start of task $t_i$ in the real coordinate system.

   7. The real duration ${\mathrm{𝑟𝑑}}_i$ corresponds to the duration of task $t_i$ including the eventual unavailability periods crossed by task $t_i$. When task $t_i$ is non-resumable (i.e., $r_i=0$) its real duration is equal to its virtual duration (i.e., ${\mathrm{𝑟𝑑}}_i={\mathrm{𝑣𝑑}}_i$).

   8. The real end ${\mathrm{𝑟𝑒}}_i$ indicates the end of task $t_i$ in the real coordinate system. We have that ${\mathrm{𝑟𝑠}}_i+{\mathrm{𝑟𝑑}}_i={\mathrm{𝑟𝑒}}_i$.

The link between the virtual starts (respectively virtual ends) and the real starts (respectively real ends) of the different tasks of $𝒯$ is ensured by a $\mathrm{𝚌𝚊𝚕𝚎𝚗𝚍𝚊𝚛}$$(\mathrm{𝙸𝙽𝚂𝚃𝙰𝙽𝚃𝚂},\mathrm{𝙼𝙰𝙲𝙷𝙸𝙽𝙴𝚂})$ constraint. More precisely, for each task $t_i$ (with $i\in [1,n]$), no matter whether it is resumable or not, we create the following items for the collection $\mathrm{𝙸𝙽𝚂𝚃𝙰𝙽𝚃𝚂}$:

The first item links the virtual and the real start of task $t_i$, while the second item relates the virtual and real ends. For each machine $m_i$ (with $i\in [1,p]$) and its corresponding list of crossable unavailability periods, denoted $\mathrm{𝑐𝑟𝑜𝑠𝑠𝑎𝑏𝑙𝑒}\_{\mathrm{𝑢𝑛𝑎𝑣𝑎𝑖𝑙𝑎𝑏𝑖𝑙𝑖𝑡𝑦}}_i$, we create the following item of the collection $\mathrm{𝙼𝙰𝙲𝙷𝙸𝙽𝙴𝚂}$:

To express the resource constraint, i.e., the fact that two tasks assigned to the same machine should not overlap in time, we use a $\mathrm{𝚐𝚎𝚘𝚜𝚝}$$(2,\mathrm{𝙾𝙱𝙹𝙴𝙲𝚃𝚂},\mathrm{𝚂𝙱𝙾𝚇𝙴𝚂})$ constraint. For each task $t_i$ (with $i\in [1,n]$) we create one item for the $\mathrm{𝙾𝙱𝙹𝙴𝙲𝚃𝚂}$ collection as well as one item for the $\mathrm{𝚂𝙱𝙾𝚇𝙴𝚂}$ collection:

The first item corresponds to an object with $i$ as unique identifier, with a rectangular shape identifier $i$ and with $m_i,{\mathrm{𝑣𝑠}}_i$ as the coordinates of its lower left corner. The second item corresponds to a rectangular shape with $i$ as unique identifier, $\langle 0,0\rangle$ as shift offset with respect to its lower left corner, and $\langle 1,{\mathrm{𝑣𝑑}}_i\rangle$ as the sizes of the rectangular shape.

Similarly, to express that each task does not overlap a non-crossable unavailability period, we create for each non-crossable unavailability period $i$ one item for the $\mathrm{𝙾𝙱𝙹𝙴𝙲𝚃𝚂}$ collection as well as one item for the $\mathrm{𝚂𝙱𝙾𝚇𝙴𝚂}$ collection:

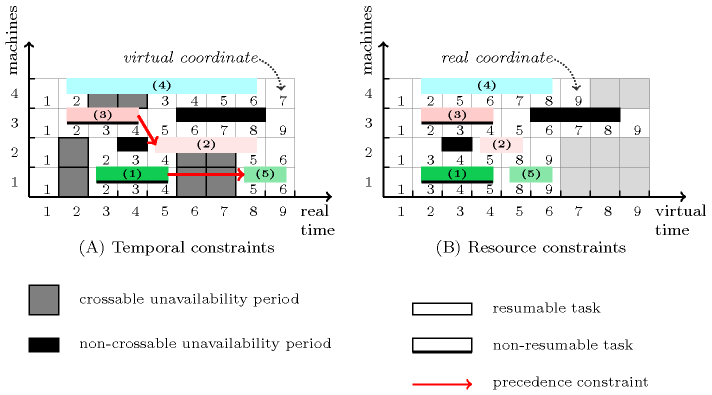
Finally, a precedence constraint between two distinct tasks $t_i$ and $t_j$ (with $i,j\in [1,n]$) is modelled by an inequality constraint between the real end of task $t_i$ and the real start of task $t_j$, namely ${\mathrm{𝑟𝑒}}_i\le {\mathrm{𝑟𝑠}}_j$. Figure 3.7.60 provides a toy example of such problem with:

• Four machines, numbered from 1 to 4, where:

  • Machine $m_1$ has two crossable unavailability periods respectively corresponding to intervals $[2,2]$ and $[6,7]$.

  • Machine $m_2$ has two crossable unavailability periods respectively corresponding to intervals $[2,2]$ and $[6,7]$, as well as one non-crossable unavailability period corresponding to interval $[3,3]$.

  • Machine $m_3$ has a single non-crossable unavailability corresponding to interval $[6,8]$.

  • Machine $m_4$ has a single crossable unavailability period corresponding to interval $[3,4]$.

• Five tasks, numbered from 1 to 5, where:

  • Task $t_1$ is a non-resumable task that has a virtual duration of 3.

  • Task $t_2$ is a resumable task that has a virtual duration of 2.

  • Task $t_3$ is a non-resumable task that has a virtual duration of 3.

  • Task $t_4$ is a resumable task that has a virtual duration of 5.

  • Task $t_5$ is a resumable task that has a virtual duration of 2.

• Finally, (1) all five tasks should not overlap, (2) task $t_3$ should precedes task $t_2$ and (3) task $t_1$ should precedes task $t_5$.

Figure 3.7.60. Illustration of the scheduling problem with crossable and non-crossable unavailability periods as well as with resumable and non-resumable tasks: part (A) gives the real time coordinate system where all precedence constraints are stated, while part (B) provides the virtual time coordinate system – from which all crossable unavailability periods are removed – where the non-overlapping constraint is stated

A survey on machine scheduling problems with unavailability constraints both in the deterministic and stochastic cases can be found in [SaidyTaghaviFard08]. Unavailability can have multiple causes such as:

• In the context of production scheduling, machine unavailability corresponds to accepted orders that were already scheduled for a given date. This can typically corresponds to unavailability periods at the beginning of the planning horizon. Preemptive maintenance can also be another cause of machine unavailability.

• In the context of timetabling, unavailability periods may come from work regulation which enforces not to work in a continuous way more than a given limit. Unavailability periods may also come from scheduled meetings during the working day.

• In the context of distributed computing where cpu time is donated for performing huge tasks, machines are typically partially available [DiedrichJansenSchwarzTrystram09].