3.7.163. n-Amazons
modelling: n-Amazons A constraint that can be used for modelling the -Amazons problem. Place Amazons on an by chessboard in such a way that no Amazon attacks another. We say that two columns (respectively two rows) of a chessboard are almost adjacent if and only if the two columns (respectively the two rows) are separated by a single column (respectively a single row). Two Amazons attack each other if at least one of the following conditions holds:
They are located on the same column, on the same row or on the same diagonal.
They are located either on adjacent columns and on almost adjacent rows, or on almost adjacent columns and on adjacent rows.
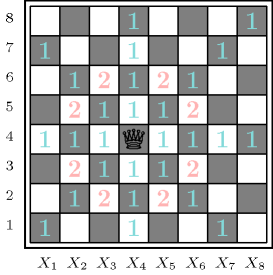
As shown by these conditions, an Amazon combines the movements of a queen and of a knight. Figure 3.7.43 illustrates the movements of an Amazon. The -Amazons problem has no solution when is smaller than 10.
Figure 3.7.43. Illustration of the moves of an Amazon: moves labelled by 1 correspond to queen's moves, while moves labelled by 2 correspond to knight's moves
We now show how to model the -Amazons problem with six global constraints. We start from the model that is used for the n-queens problem. We associate to the column of the chessboard a domain variable that gives the row number where the corresponding queen is located.
The fact that two Amazons should not be located on the same column, on the same row or on the same diagonal can be modelled as the conjunction of three constraints:
The fact that two Amazons cannot both be located on adjacent columns and on almost adjacent rows can be modelled by disequality constraints of the form .
Similarly, the fact that two Amazons cannot both be located on almost adjacent columns and on adjacent rows can be modelled by disequality constraints of the form . For a reason that will become clear later on, we rewrite this set of disequalities as and .
If we combine the constraints of the form with the three constraints we get the conjunction of constraints . This conjunction of three disequalities can be expressed as a single inequality of the form . Furthermore all these inequalities can be combined into a single constraint of the form .Since we enforce for all pairs of consecutive variables , the constraint , the name seems odd. However the name stands from the situation where the number of inequalities constraints should be minimised. Similarly we get the constraints and . Again we obtain two constraints of the form and .
Finally, the constraint can also be used as a channelling constraint if we want to create an additional variable for each row. This may be for instance the case if we want to have a heuristics for selecting first the column or the row that has the smallest number of possibilities.
Figure 3.7.44. The unique solution to the 10-Amazons problem (modulo symmetries)

Figure 3.7.44 shows the unique solution, modulo symmetries, to the -Amazons problem for . We have the following conjunction of constraints: