3.7.104. Floor planning problem
A constraint that can be used for the floor planning problem. The floor planning problem [Pfefferkorn75], [Tong87], [Maculet91], [Charman95], [Medjdoub96] involves various type of spaces, such as the placement space itself (i.e., the floor), the rooms to place within the placement space, and the circulation between the rooms. The placement space can be located on a single level or on several levels. Very often the placement space corresponds to a single rectangle and all rooms are rectangles with their borders parallel to the contour of the placement space. Circulation typically corresponds to corridors or stairs that respectively allow to access from one room to another room or from one level to another level. Within the context of floor planning three main classes of constraints have been identified [MedjdoubYannou00], namely dimensional topological and implicit constraints:
A dimensional constraint usually restricts the length, the width or the surface of a single space. Ratio constraints enforce aesthetic proportions between the length and the width of a single space or constraint the surfaces of two closely related spaces such as the toilets and the shower. Dimensional constraints can be expressed by reducing the domain of some variable or by stating some arithmetic constraints between two variables.
A topological constraint imposes a condition between two spaces. Typical topological constraints are:
Adjacency constraints with a minimum contact between a room and a corridor or another room allow expressing that there must be enough place to put a door between two given spaces. In the context of staircases one has to enforce that fact that the first and last stairs are completely accessible. When a corridor is made up from two parts, one also has to enforce that the two parts are fully in contact.
Adjacency with the contour constraints between a room and a specified (or not) side of the contour allow expressing the orientation of a room (or just that a room must have some window).
Relative positioning constraints between two specified rooms allow for instance expressing the fact that a room is located to the north of another room.
Minimum and maximum distance constraints between two rooms allow expressing the proximity between two given rooms.
Topological constraints occur naturally in the preliminary design phase in architecture and can typically be expressed by using reified or global constraints.
An implicit constraint puts a global condition that is inherent to floor planning problems between all the spaces of the floor. We typically have:
Inclusion of each room and circulation within the contour.
Partitioning of the placement space (i.e., no wasted space is permitted). This is usually a hard constraint which requires specific propagation in order to prevent the creation of wasted space.
Non-overlapping between rooms.
Symmetry breaking constraints between identical rooms imposes for instance a lexicographic order between their respective lower leftmost corners.
Such constraints can typically be expressed by using global constraints, such as , , or .
Finally, in order to allocate as much surface as possible to the rooms, one wants sometimes to minimise the total circulation area between the different rooms.
Figure 3.7.27. A solution to Maculet floor planning problem which minimises the total area of the corridors
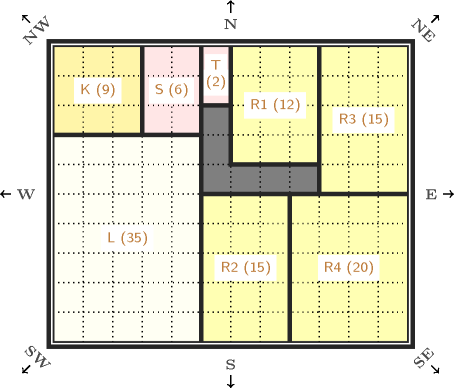
In order to illustrate these constraints we now consider an example of floor planning problem taken from R. Maculet PhD thesis [Maculet91] involving 11 spaces. Constraints on the dimensions of these space are:
The floor where to place everything has a size of 12 by 10 meters.
The living has a surface between 33 and 42 square meters and a minimum size of 4 by 4.
The kitchen has a surface between 9 and 15 square meters and a minimum size of 3 by 3.
The shower has a surface between 6 and 9 square meters and a minimum size of 2 by 2.
The toilet has a surface between 1 and 2 square meters and a minimum size of 1 by 1.
The first and second parts of the corridor have both a surface between 1 and 12 square meters and a minimum size of 1 by 1.
The first, second and third rooms have all a surface between 11 and 15 square meters and a minimum size of 3 by 3.
The fourth room has a surface between 15 and 20 square meters and a minimum size of 3 by 3.
Topological constraints between spaces are:
The living is located on the south-west contour. The kitchen, the first, second and third rooms are either located on the south or on the north contour. The fourth room is on the south contour.
All spaces, except the kitchen, are adjacent to one of the corridors with at least 1 meter of full contact.
The kitchen is adjacent to the living and to the shower.
The toilet is adjacent to the kitchen or to the shower.
The first and the second parts of the corridor are adjacent and fully in contact.
Finally no wasted space is permitted. Figure 3.7.27 presents a solution to the corresponding floor planning problem that minimises the area of the two corridors.