3.7.178. Packing almost squares
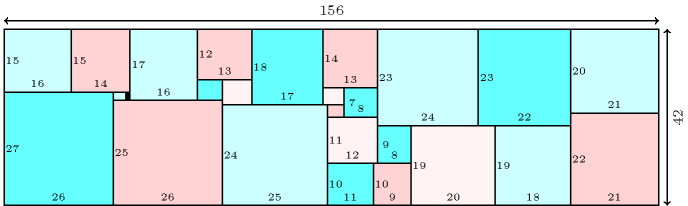
Denotes that a constraint can be used for solving the packing almost squares problem: tile a rectangle for which sides are consecutive integers by rectangles of size which can be rotated by 90 degrees. The problem is described in http://www.stetson.edu/~efriedma/almost/. Since there does not always exist a tiling, one can also consider a variant where the goal is to find the rectangle with minimal area. Figure 3.7.48 provides a solution for found by H. Simonis.
Figure 3.7.48. A solution to the packing almost squares problem for ; the width and the height of each not too small rectangle are respectively shown on the lowest and leftmost borders of the rectangle.