3.7.90. Domination

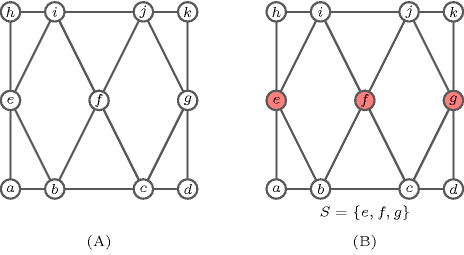
A constraint that can be used for expressing directly the fact that we search for a dominating set in an undirected graph. Given an undirected graph G=(V,E) where V is a finite set of vertices and E a finite set of unordered pairs of distinct elements from V, a set S is a dominating set if for every vertex u∈V-S there exists a vertex v∈S such that u is adjacent to v. Part (A) of Figure 3.7.26 gives an undirected graph G, while part (B) depicts a dominating set S={e,f,g} in G.

Figure 3.7.26. (A)Β A graph and (B)Β one of its dominating set S={e,f,g}
ctrs/preface-166-tikz