3.7.235. Smallest rectangle area
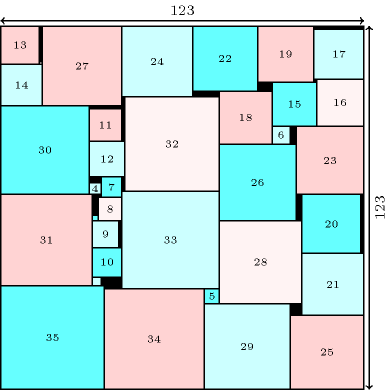
Denotes that a constraint can be used for finding the smallest rectangle area where one can pack a given set of rectangles (or squares). A first example of such packing problem attributed to S. W. Golomb is to find the smallest square that can contain the set of consecutive squares from up to so that these squares do not overlap each other. A program using the constraint was used to construct such a table for in [BeldiceanuBourreauChanRivreau97]. New optimal solutions for this problem were found in [SimonisSullivan08] for . Figure 3.7.66 gives the solution found for by H. Simonis and B. O'Sullivan. Algorithms and lower bounds for solving the same problem can also be respectively found in [CapraraLodiMartelloMonaci06] and in [Korf04].
Figure 3.7.66. Smallest square (of size 123) for packing squares of size
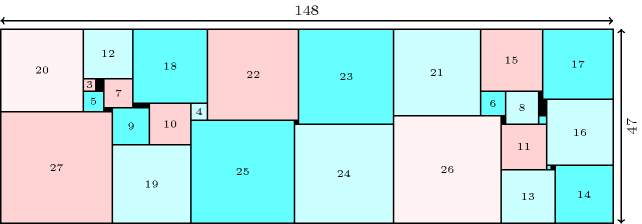
In his paper (i.e., [Korf04]), Richard E. Korf also considers the problem of finding the minimum-area rectangle that can contain the set of consecutive squares from up to and solve it up to . In 2008 this value was improved up to by H. Simonis and B. O'Sullivan [SimonisSullivan08]. Figure 3.7.67 gives the solution found for by H. Simonis and B. O'Sullivan.
Figure 3.7.67. Rectangle with the smallest surface (of size ) for packing squares of size