3.7.196. Producer-consumer
A constraint that can be used for modelling problems where a first set of tasks produces a non-renewable resource, while a second set of tasks consumes this resource so that a limit on the minimum or the maximum stock at each instant is imposed.
Parts (A) and (B) of Figure 3.7.52 describes the simplest variant of the producer-consumer problem [SimonisCornelissens95] where no negative stock is allowed. Given an initial stock, a first set of tasks (i.e., producers) add instantaneously their respective productions to the stock (when they are finished), and a second set of tasks (i.e., consumers) take instantaneously from the stock (when they start) the amount of non-renewable resource they need. The problem is to schedule these tasks (i.e., fix the end of the producers and fix the start of the consumers) and to fix for each task the quantity it produces or consumes, so that no negative stock occurs. Part (A) of Figure 3.7.52 describes an instance of such problem where we respectively have 2 producers and 3 consumers. Part (B) depicts the corresponding cumulative view of the problem. At each timepoint the difference between the top line and the top of the cumulated profile gives the amount of available stock at that timepoint.
Figure 3.7.52. Producer-consumer models (A,C) and corresponding views (B,D) enforcing that, at any point in time, we do not have any negative stock, i.e. at any point in time we do not consume more that we have produced so far; (E) constraint associated with (B)
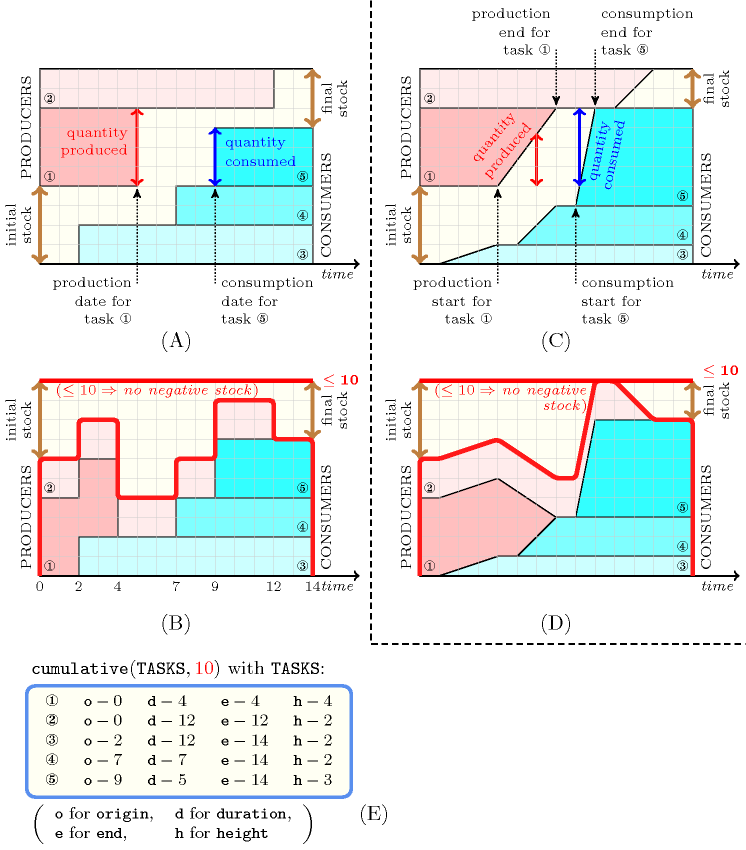
A fundamental problem with the previous variant of the producer-consumer problem is that it does not allow to handle the fact that a resource is produced or used gradually. Parts (C) and (D) of Figure 3.7.52 describes a second variant where this is in fact possible. This is achieved by replacing the rectangle associated with a producer by a task with a decreasing height. At a given instant the cumulated quantity produced by a producer is the difference between the height of that task at its starting time and the height of that task at the considered instant. Conversely a consumer is modelled by a task with an increasing height. At a particular timepoint the cumulated quantity used by a consumer task is the difference between the height of that task at its end and the height of that task at the considered instant. Part (C) of Figure 3.7.52 describes an instance of such problem where, again, we respectively have 2 producers and 3 consumers. Part (D) depicts the corresponding cumulative view of the problem. As before, at each timepoint the difference between the top line and the top of the cumulated profile gives the amount of available stock at that timepoint.