3.7.243. Squared squares
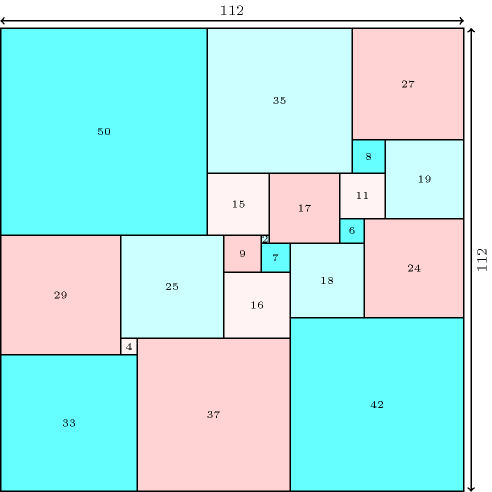
A constraint that can be used for modelling the squared squares problem [CroftFalconerGuy91] [LintWilson92] (also called the perfect squared squares problem [Duijvestijn78]): a perfect squared square of order is a square that can be tiled with smaller squares such that each of the smaller squares has a different integer size. It is called simple if it does not contain a subset of at least two squares, corresponding to a square or to a rectangle. Duijvestijn has shown in 1962 that no instances exist with less than 21 squares [Duijvestijn78]. A single solution depicted by Figure 3.7.71 exists with 21 squares, where the squares have sizes 2, 4, 6, 7, 8, 9, 11, 15, 16, 17, 18, 19, 24, 25, 27, 29, 33, 35, 37, 42, 50 and must be packed into a square of size 112.
Figure 3.7.71. A simple perfect squared square of order 21
A catalogue of such simple squared squares of orders 21 through 25 is provided in [BouwkampDuijvestijn92]. The following table contains all the problem instances from the previous catalogue. The different fields respectively give the problem number, the number of squares, the size of the master square and a list of the square sizes. The two last columns present a solution as a ground instance of geost, and a graphical view (see the description below). Problems 166 and 167, 168 and 169, 182 and 183 are identical, but have two non-isomorphic solutions. A much bigger table can be found at the following link http://www.squaring.net/.
When the size of the squares is known four constraint programming approach are respectively reported in [AggounBeldiceanu93], in [VanHentenryck94], in [SimonisBourreauBeldiceanu99], in [BeldiceanuCarlssonPoderSadekTruchet07] and in [BeldiceanuCarlssonPoder08].
| 1 | 21 | 112 | 2,4,6,7,8,9,11,15,16,17,18,19,24,25,27,29,33,35,37,42,50 | sol | view |
| 2 | 22 | 110 | 2,3,4,6,7,8,12,13,14,15,16,17,18,21,22,23,24,26,27,28,50,60 | sol | view |
| 3 | 22 | 110 | 1,2,3,4,6,8,9,12,14,16,17,18,19,21,22,23,24,26,27,28,50,60 | sol | view |
| 4 | 22 | 139 | 1,2,3,4,7,8,10,17,18,20,21,22,24,27,28,29,30,31,32,38,59,80 | sol | view |
| 5 | 22 | 147 | 1,3,4,5,8,9,17,20,21,23,25,26,29,31,32,40,43,44,47,48,52,55 | sol | view |
| 6 | 22 | 147 | 2,4,8,10,11,12,15,19,21,22,23,25,26,32,34,37,41,43,45,47,55,59 | sol | view |
| 7 | 22 | 154 | 2,5,9,11,16,17,19,21,22,24,26,30,31,33,35,36,41,46,47,50,52,61 | sol | view |
| 8 | 22 | 172 | 1,2,3,4,9,11,13,16,17,18,19,22,24,33,36,38,39,42,44,53,75,97 | sol | view |
| 9 | 22 | 192 | 4,8,9,10,12,14,17,19,26,28,31,35,36,37,41,47,49,57,59,62,71,86 | sol | view |
| 10 | 23 | 110 | 1,2,3,4,5,7,8,10,12,13,14,15,16,19,21,28,29,31,32,37,38,41,44 | sol | view |
| 11 | 23 | 139 | 1,2,7,8,12,13,14,15,16,18,19,20,21,22,24,26,27,28,32,33,38,59,80 | sol | view |
| 12 | 23 | 140 | 1,2,3,4,5,8,10,13,16,19,20,23,27,28,29,31,33,38,42,45,48,53,54 | sol | view |
| 13 | 23 | 140 | 2,3,4,7,8,9,12,15,16,18,22,23,24,26,28,30,33,36,43,44,47,50,60 | sol | view |
| 14 | 23 | 145 | 1,2,3,4,6,8,9,12,15,20,22,24,25,26,27,29,30,31,32,34,36,61,84 | sol | view |
| 15 | 23 | 180 | 2,4,8,10,11,12,15,19,21,22,23,25,26,32,33,34,37,41,43,45,47,88,92 | sol | view |
| 16 | 23 | 188 | 2,4,8,10,11,12,15,19,21,22,23,25,26,32,33,34,37,45,47,49,51,92,96 | sol | view |
| 17 | 23 | 208 | 1,3,4,9,10,11,12,16,17,18,22,23,24,40,41,60,62,65,67,70,71,73,75 | sol | view |
| 18 | 23 | 215 | 1,3,4,9,10,11,12,16,17,18,22,23,24,40,41,60,66,68,70,71,74,76,79 | sol | view |
| 19 | 23 | 228 | 2,7,9,10,15,16,17,18,22,23,25,28,36,39,42,56,57,68,69,72,73,87,99 | sol | view |
| 20 | 23 | 257 | 2,3,9,11,14,15,17,20,22,24,28,29,32,33,49,55,57,60,63,66,79,123,134 | sol | view |
| 21 | 23 | 332 | 1,15,17,24,26,30,31,38,47,48,49,50,53,56,58,68,83,89,91,112,120,123,129 | sol | view |
| 22 | 24 | 120 | 3,4,5,6,8,9,10,12,13,14,15,16,17,19,20,23,25,32,33,34,40,41,46,47 | sol | view |
| 23 | 24 | 186 | 2,3,4,7,8,9,12,15,16,18,22,23,24,26,28,30,33,36,43,46,47,60,90,96 | sol | view |
| 24 | 24 | 194 | 2,3,7,9,10,16,17,18,19,20,23,25,28,34,36,37,42,53,54,61,65,68,69,72 | sol | view |
| 25 | 24 | 195 | 2,4,7,10,11,16,17,18,21,26,27,30,39,41,42,45,47,49,52,53,54,61,63,80 | sol | view |
| 26 | 24 | 196 | 1,2,5,10,11,15,17,18,20,21,24,26,29,31,32,34,36,40,44,47,48,51,91,105 | sol | view |
| 27 | 24 | 201 | 1,3,4,6,9,10,11,12,17,18,20,21,22,23,26,38,40,46,50,52,53,58,98,103 | sol | view |
| 28 | 24 | 201 | 1,4,5,8,9,10,11,15,16,18,19,20,22,24,26,39,42,44,49,52,54,56,93,108 | sol | view |
| 29 | 24 | 203 | 1,2,5,10,11,15,17,18,20,21,24,26,29,31,32,34,36,40,44,48,54,58,98,105 | sol | view |
| 30 | 24 | 247 | 3,5,6,9,12,14,19,23,24,25,28,32,34,36,40,45,46,48,56,62,63,66,111,136 | sol | view |
| 31 | 24 | 253 | 2,4,5,9,13,18,20,23,24,27,28,31,38,40,44,50,61,70,72,77,79,86,88,104 | sol | view |
| 32 | 24 | 255 | 3,5,10,11,16,17,20,22,23,25,26,27,28,32,41,44,52,53,59,63,65,74,118,137 | sol | view |
| 33 | 24 | 288 | 2,7,9,10,15,16,17,18,22,23,25,28,36,39,42,56,57,60,68,72,73,87,129,159 | sol | view |
| 34 | 24 | 288 | 1,5,7,8,9,14,17,20,21,26,30,32,34,36,48,51,54,59,64,69,72,93,123,165 | sol | view |
| 35 | 24 | 290 | 2,3,8,9,11,12,14,17,21,30,31,33,40,42,45,48,59,61,63,65,82,84,124,166 | sol | view |
| 36 | 24 | 292 | 1,2,3,8,12,15,16,17,20,22,24,26,29,33,44,54,57,60,63,67,73,102,117,175 | sol | view |
| 37 | 24 | 304 | 3,5,7,11,12,17,20,22,25,29,35,47,48,55,56,57,69,72,76,92,96,100,116,132 | sol | view |
| 38 | 24 | 304 | 3,4,7,12,16,20,23,24,27,28,30,32,33,36,37,44,53,57,72,76,85,99,129,175 | sol | view |
| 39 | 24 | 314 | 2,4,11,12,16,17,18,19,28,29,40,44,47,59,62,64,65,78,79,96,97,105,113,139 | sol | view |
| 40 | 24 | 316 | 3,9,10,12,13,14,15,23,24,33,36,37,48,52,54,55,57,65,66,78,79,93,144,172 | sol | view |
| 41 | 24 | 326 | 1,6,10,11,14,15,18,24,29,32,43,44,53,56,63,65,71,80,83,101,104,106,119,142 | sol | view |
| 42 | 24 | 423 | 2,9,15,17,27,29,31,32,33,36,47,49,50,60,62,77,105,114,123,127,128,132,168,186 | sol | view |
| 43 | 24 | 435 | 1,2,8,10,13,19,23,33,44,45,56,74,76,78,80,88,93,100,112,131,142,143,150,192 | sol | view |
| 44 | 24 | 435 | 3,5,9,11,12,21,24,27,30,44,45,50,54,55,63,95,101,112,117,123,134,140,178,200 | sol | view |
| 45 | 24 | 459 | 8,9,10,11,16,30,36,38,45,55,57,65,68,84,95,98,100,116,117,126,135,144,180,198 | sol | view |
| 46 | 24 | 459 | 4,6,9,10,17,21,23,25,31,33,36,38,45,50,83,115,117,126,133,135,144,146,180,198 | sol | view |
| 47 | 24 | 479 | 5,6,17,23,24,26,28,29,35,43,44,52,60,68,77,86,130,140,150,155,160,164,174,175 | sol | view |
| 48 | 25 | 147 | 3,4,5,6,8,9,10,12,13,14,15,16,17,19,20,23,25,27,32,33,34,40,41,73,74 | sol | view |
| 49 | 25 | 208 | 1,2,3,4,5,7,8,11,12,17,18,24,26,28,29,30,36,39,44,45,50,59,60,89,119 | sol | view |
| 50 | 25 | 213 | 3,5,6,7,13,16,17,20,21,23,24,25,26,28,31,35,36,47,49,56,58,74,76,81,90 | sol | view |
| 51 | 25 | 215 | 1,4,6,7,11,15,24,26,27,33,37,39,40,41,42,43,45,47,51,55,60,62,63,69,83 | sol | view |
| 52 | 25 | 216 | 1,2,3,4,5,7,8,11,16,17,18,19,25,30,32,33,39,41,45,49,54,59,64,103,113 | sol | view |
| 53 | 25 | 236 | 1,2,4,9,11,12,13,14,15,16,19,24,38,40,44,46,47,48,59,64,65,70,81,85,107 | sol | view |
| 54 | 25 | 242 | 1,3,6,7,9,13,14,16,17,19,23,25,26,28,30,31,47,51,54,57,60,64,67,111,131 | sol | view |
| 55 | 25 | 244 | 1,2,4,5,7,10,15,17,19,20,21,22,26,27,30,37,40,41,45,65,66,68,70,110,134 | sol | view |
| 56 | 25 | 252 | 4,7,10,11,12,13,23,25,29,31,32,34,36,37,38,40,42,44,62,67,68,71,77,108,113 | sol | view |
| 57 | 25 | 253 | 2,4,5,6,9,10,12,14,20,24,27,35,36,37,38,42,43,45,50,54,63,66,70,120,133 | sol | view |
| 58 | 25 | 260 | 1,4,6,7,10,15,24,26,27,28,29,31,33,34,37,38,44,65,70,71,77,78,83,100,112 | sol | view |
| 59 | 25 | 264 | 3,7,8,12,16,18,19,20,22,24,26,31,34,37,38,40,42,53,54,61,64,69,70,130,134 | sol | view |
| 60 | 25 | 264 | 3,8,12,13,16,18,20,21,22,24,26,29,34,38,40,42,43,47,54,59,64,70,71,130,134 | sol | view |
| 61 | 25 | 264 | 1,3,4,6,9,10,11,12,16,17,18,20,21,22,39,42,54,56,61,66,68,69,73,129,135 | sol | view |
| 62 | 25 | 265 | 1,3,4,6,9,10,11,12,16,17,18,20,21,22,39,42,54,56,62,66,68,69,74,130,135 | sol | view |
| 63 | 25 | 273 | 1,4,8,10,11,12,17,19,21,22,27,29,30,33,37,43,52,62,65,86,88,89,91,96,120 | sol | view |
| 64 | 25 | 273 | 1,6,9,14,16,17,18,21,22,23,25,31,32,38,44,46,48,50,54,62,65,68,78,133,140 | sol | view |
| 65 | 25 | 275 | 2,3,7,13,17,24,25,31,33,34,35,37,41,49,51,53,55,60,68,71,74,81,94,100,107 | sol | view |
| 66 | 25 | 276 | 1,5,8,9,11,18,19,21,30,36,41,44,45,46,47,51,53,58,63,69,71,84,87,105,120 | sol | view |
| 67 | 25 | 280 | 5,6,11,17,18,20,21,24,27,28,32,34,41,42,50,53,54,55,68,78,85,88,95,97,117 | sol | view |
| 68 | 25 | 280 | 2,3,7,8,14,18,30,36,37,39,44,50,52,54,56,60,63,64,65,72,75,78,79,96,106 | sol | view |
| 69 | 25 | 284 | 1,2,11,12,14,16,18,19,23,26,29,37,38,39,40,42,59,68,69,77,78,97,106,109,110 | sol | view |
| 70 | 25 | 286 | 1,4,5,7,10,12,15,16,20,23,28,30,32,33,35,37,53,54,64,68,74,79,80,133,153 | sol | view |
| 71 | 25 | 289 | 2,3,5,8,13,14,17,20,21,32,36,41,50,52,60,61,62,68,74,76,83,87,100,102,104 | sol | view |
| 72 | 25 | 289 | 2,3,4,5,7,12,16,17,19,21,23,25,29,31,32,44,57,64,65,68,72,76,84,140,149 | sol | view |
| 73 | 25 | 290 | 1,2,10,11,13,14,15,17,18,28,29,34,36,38,50,56,60,69,77,80,85,91,94,111,119 | sol | view |
| 74 | 25 | 293 | 5,6,11,17,18,20,21,24,27,28,32,34,41,42,50,54,55,66,68,78,85,88,95,110,130 | sol | view |
| 75 | 25 | 297 | 2,7,8,9,10,15,16,17,18,23,25,26,28,36,38,43,53,60,61,68,69,77,99,137,160 | sol | view |
| 76 | 25 | 308 | 1,3,4,7,10,12,13,23,25,34,37,38,39,43,44,45,62,77,79,85,87,108,113,115,116 | sol | view |
| 77 | 25 | 308 | 1,5,6,7,8,9,13,16,19,28,33,36,38,43,45,48,70,71,73,84,86,102,104,120,133 | sol | view |
| 78 | 25 | 309 | 7,8,14,16,23,24,25,26,31,33,34,39,48,56,59,60,62,70,76,82,92,100,101,108,117 | sol | view |
| 79 | 25 | 311 | 2,7,8,9,10,15,16,17,18,23,25,26,28,36,38,43,53,60,61,68,83,91,99,151,160 | sol | view |
| 80 | 25 | 314 | 1,6,7,11,16,22,26,29,32,36,38,44,51,53,64,69,70,73,74,75,85,87,101,116,128 | sol | view |
| 81 | 25 | 316 | 1,3,9,12,21,26,30,33,34,35,38,39,40,41,53,56,59,69,79,85,96,103,111,117,120 | sol | view |
| 82 | 25 | 317 | 1,5,6,7,8,9,16,17,19,32,37,40,42,47,49,52,59,75,81,92,94,110,112,113,126 | sol | view |
| 83 | 25 | 320 | 2,7,8,9,12,14,15,21,23,35,38,44,46,49,53,54,56,63,96,101,103,105,108,112,116 | sol | view |
| 84 | 25 | 320 | 3,8,9,11,17,18,22,25,26,27,29,30,31,33,35,49,51,67,72,73,80,85,95,152,168 | sol | view |
| 85 | 25 | 320 | 1,4,6,7,8,13,14,16,24,28,30,33,34,38,41,42,57,60,69,78,81,90,92,150,170 | sol | view |
| 86 | 25 | 320 | 3,4,6,8,9,14,15,16,24,28,30,31,34,38,39,42,59,60,71,78,79,90,92,150,170 | sol | view |
| 87 | 25 | 322 | 3,4,8,9,10,16,18,20,22,23,24,28,31,38,44,47,64,65,68,76,80,81,97,144,178 | sol | view |
| 88 | 25 | 322 | 3,4,8,10,15,16,18,19,20,22,24,28,35,38,44,53,59,64,68,76,80,85,93,144,178 | sol | view |
| 89 | 25 | 323 | 2,3,4,7,10,13,15,18,23,32,34,35,36,42,46,50,57,60,66,72,78,87,98,159,164 | sol | view |
| 90 | 25 | 323 | 3,8,9,11,17,18,22,25,26,27,29,30,31,33,35,49,51,67,72,73,83,88,95,155,168 | sol | view |
| 91 | 25 | 323 | 2,6,9,11,13,14,18,19,20,23,27,28,29,42,46,48,60,64,72,74,79,82,98,146,177 | sol | view |
| 92 | 25 | 325 | 3,5,6,11,12,13,18,23,25,28,32,37,40,43,45,46,51,79,92,99,103,108,112,114,134 | sol | view |
| 93 | 25 | 326 | 1,4,8,10,12,16,21,22,24,27,28,35,36,37,38,46,49,68,70,75,88,90,93,158,168 | sol | view |
| 94 | 25 | 327 | 2,9,10,12,13,16,19,21,23,26,36,44,46,52,55,61,62,74,84,87,100,103,104,120,140 | sol | view |
| 95 | 25 | 328 | 2,3,4,7,8,10,14,17,26,27,28,36,38,40,42,45,53,58,73,74,79,94,102,152,176 | sol | view |
| 96 | 25 | 334 | 1,4,8,10,12,16,21,22,24,27,28,35,36,37,38,46,49,68,75,78,88,93,98,166,168 | sol | view |
| 97 | 25 | 336 | 2,3,4,7,8,10,14,17,26,27,28,36,38,40,45,50,53,58,73,74,79,94,110,152,184 | sol | view |
| 98 | 25 | 338 | 1,4,8,10,12,16,19,22,24,25,28,36,37,38,39,46,53,68,70,73,94,96,101,164,174 | sol | view |
| 99 | 25 | 338 | 4,5,8,10,12,15,16,21,22,24,28,33,36,38,43,46,57,68,70,77,94,96,97,164,174 | sol | view |
| 100 | 25 | 340 | 1,4,5,6,11,13,16,17,22,24,44,46,50,51,52,53,61,64,66,79,84,85,92,169,171 | sol | view |
| 101 | 25 | 344 | 2,3,8,11,14,17,19,21,23,25,27,36,39,44,48,53,56,71,77,83,86,89,98,169,175 | sol | view |
| 102 | 25 | 359 | 7,8,9,10,14,17,18,23,25,27,29,31,40,41,43,46,69,74,82,85,90,98,102,172,187 | sol | view |
| 103 | 25 | 361 | 2,6,7,8,9,14,20,22,26,27,32,34,36,47,49,56,66,67,74,82,89,98,107,156,205 | sol | view |
| 104 | 25 | 363 | 1,4,6,12,13,20,21,25,26,27,28,32,37,41,45,53,58,64,69,91,97,102,106,155,208 | sol | view |
| 105 | 25 | 364 | 2,3,4,6,8,9,13,14,16,19,23,24,28,29,52,57,64,75,82,91,98,100,109,173,191 | sol | view |
| 106 | 25 | 367 | 1,4,6,12,13,20,21,25,26,27,28,32,37,41,49,53,58,64,69,91,97,102,110,155,212 | sol | view |
| 107 | 25 | 368 | 1,6,15,16,17,18,22,25,31,33,39,42,45,46,47,48,51,69,72,88,91,96,112,160,208 | sol | view |
| 108 | 25 | 371 | 1,2,7,8,20,21,22,24,26,28,30,38,43,46,50,51,64,65,70,90,95,102,109,160,211 | sol | view |
| 109 | 25 | 373 | 3,6,7,8,15,17,22,23,31,32,35,41,43,60,62,68,79,87,104,105,114,120,121,138,148 | sol | view |
| 110 | 25 | 378 | 2,3,10,17,18,20,21,22,24,27,31,38,41,48,51,56,68,78,80,85,87,96,117,165,213 | sol | view |
| 111 | 25 | 378 | 1,2,7,13,15,17,18,25,27,29,30,31,42,43,46,56,61,68,73,93,100,105,112,161,217 | sol | view |
| 112 | 25 | 380 | 4,7,17,18,19,20,21,26,31,33,35,40,45,48,49,60,67,73,79,81,87,107,113,186,194 | sol | view |
| 113 | 25 | 380 | 4,5,6,9,13,15,16,17,22,24,33,38,44,49,50,56,60,67,82,84,95,108,121,177,203 | sol | view |
| 114 | 25 | 381 | 12,13,21,23,25,27,35,36,42,45,54,57,59,60,79,82,84,85,92,95,96,100,110,111,186 | sol | view |
| 115 | 25 | 384 | 1,4,8,9,11,12,19,21,27,32,35,44,45,46,47,51,60,67,84,89,96,108,120,180,204 | sol | view |
| 116 | 25 | 384 | 1,4,8,9,11,12,15,17,19,25,26,31,32,37,44,57,60,81,84,96,99,108,120,180,204 | sol | view |
| 117 | 25 | 384 | 3,5,7,11,12,17,20,22,25,29,35,47,48,55,56,57,69,72,76,80,96,100,116,172,212 | sol | view |
| 118 | 25 | 385 | 1,2,7,13,15,17,18,25,27,29,30,31,43,46,49,56,61,68,73,93,100,105,119,161,224 | sol | view |
| 119 | 25 | 392 | 4,7,8,15,23,26,29,30,31,32,34,43,48,55,56,68,77,88,98,106,116,135,141,151,153 | sol | view |
| 120 | 25 | 392 | 10,12,14,16,19,21,25,27,31,35,39,41,51,52,54,55,73,92,98,115,121,123,129,148,171 | sol | view |
| 121 | 25 | 392 | 1,4,5,8,11,14,16,21,22,24,27,28,30,31,52,64,81,83,96,97,98,99,114,195,197 | sol | view |
| 122 | 25 | 393 | 4,8,16,20,23,24,25,27,29,37,44,45,50,53,64,66,68,69,73,85,91,101,116,186,207 | sol | view |
| 123 | 25 | 396 | 1,4,5,14,16,32,35,36,46,47,48,49,68,69,73,93,94,97,99,104,110,111,125,126,160 | sol | view |
| 124 | 25 | 396 | 1,4,5,8,11,14,16,21,22,24,27,28,30,31,52,64,81,83,98,99,100,101,114,197,199 | sol | view |
| 125 | 25 | 396 | 3,8,9,11,14,16,17,18,31,32,41,45,48,56,60,66,73,75,81,82,98,99,117,180,216 | sol | view |
| 126 | 25 | 398 | 2,6,7,11,15,17,23,28,29,39,44,46,53,56,58,65,68,99,100,119,120,134,144,145,154 | sol | view |
| 127 | 25 | 400 | 3,6,21,23,24,26,29,35,37,40,41,47,53,55,64,76,79,81,99,100,121,122,137,142,179 | sol | view |
| 128 | 25 | 404 | 3,6,7,14,17,20,21,26,28,31,32,39,46,53,54,68,71,80,88,92,100,111,113,199,205 | sol | view |
| 129 | 25 | 404 | 4,7,10,11,12,13,16,18,20,23,25,28,29,32,47,62,70,88,93,96,101,114,127,189,215 | sol | view |
| 130 | 25 | 408 | 2,3,7,13,16,18,20,27,30,33,41,43,46,52,54,57,72,79,84,100,105,108,116,195,213 | sol | view |
| 131 | 25 | 412 | 3,11,12,15,21,26,32,39,43,47,54,60,68,73,83,85,86,87,89,99,114,129,139,144,169 | sol | view |
| 132 | 25 | 413 | 5,7,17,20,34,38,39,48,56,57,59,60,64,65,70,72,75,81,105,106,110,125,148,153,155 | sol | view |
| 133 | 25 | 416 | 2,4,7,11,13,24,25,30,35,37,39,40,44,58,62,65,82,104,112,120,128,135,143,153,169 | sol | view |
| 134 | 25 | 416 | 1,2,3,8,12,15,16,17,20,22,24,26,29,31,64,75,85,88,91,94,98,104,133,179,237 | sol | view |
| 135 | 25 | 421 | 1,2,4,5,7,9,12,16,20,22,23,35,38,48,56,83,94,104,116,118,128,140,150,153,177 | sol | view |
| 136 | 25 | 421 | 5,11,12,17,18,20,23,26,29,36,38,40,44,51,55,59,72,92,97,102,105,107,117,199,222 | sol | view |
| 137 | 25 | 422 | 2,4,7,13,16,18,20,23,28,29,38,43,46,51,59,68,74,79,86,93,100,111,132,179,243 | sol | view |
| 138 | 25 | 425 | 3,4,5,9,10,12,13,14,16,19,20,31,46,48,56,79,102,104,116,126,128,140,142,157,181 | sol | view |
| 139 | 25 | 441 | 5,6,7,16,18,23,24,27,38,39,47,51,52,62,66,72,80,84,92,101,102,118,120,219,222 | sol | view |
| 140 | 25 | 454 | 1,2,11,17,29,34,35,46,48,51,53,55,63,69,79,87,88,91,109,134,136,143,150,161,184 | sol | view |
| 141 | 25 | 456 | 5,7,10,11,13,15,18,19,31,49,50,52,59,60,63,72,77,115,128,129,135,142,148,179,193 | sol | view |
| 142 | 25 | 465 | 6,9,13,14,19,21,24,25,31,32,53,56,64,73,74,82,91,111,125,127,137,139,153,173,201 | sol | view |
| 143 | 25 | 472 | 7,9,13,15,26,34,35,44,47,51,58,61,65,81,87,103,104,115,118,123,128,133,136,148,221 | sol | view |
| 144 | 25 | 477 | 3,5,12,16,19,22,25,26,37,41,49,72,76,77,82,86,87,115,117,135,141,149,167,169,193 | sol | view |
| 145 | 25 | 492 | 2,9,15,17,27,29,31,32,33,36,47,49,50,60,62,69,77,105,114,123,127,128,132,237,255 | sol | view |
| 146 | 25 | 492 | 3,5,9,11,12,21,24,27,30,44,45,50,54,55,57,63,95,101,112,117,123,134,140,235,257 | sol | view |
| 147 | 25 | 503 | 4,15,16,19,22,23,25,27,33,34,50,62,67,87,88,93,100,113,135,143,149,157,167,179,211 | sol | view |
| 148 | 25 | 506 | 1,7,24,26,33,35,40,45,47,51,55,69,87,90,93,96,117,125,134,145,146,147,160,162,199 | sol | view |
| 149 | 25 | 507 | 2,3,7,11,13,15,28,34,43,50,57,64,80,83,86,89,107,115,116,127,149,163,175,183,217 | sol | view |
| 150 | 25 | 512 | 1,7,8,9,10,15,22,32,34,46,51,65,69,71,91,105,109,111,136,139,152,157,173,200,203 | sol | view |
| 151 | 25 | 512 | 1,6,7,8,9,13,17,19,35,45,47,57,62,73,88,93,104,107,128,130,151,163,184,198,221 | sol | view |
| 152 | 25 | 513 | 6,9,10,17,19,24,28,29,37,39,64,65,68,81,98,99,102,115,145,147,153,159,165,189,201 | sol | view |
| 153 | 25 | 517 | 5,6,7,16,20,24,28,33,38,43,63,71,80,83,86,92,98,122,132,148,164,166,173,180,205 | sol | view |
| 154 | 25 | 524 | 9,12,20,21,33,35,37,39,54,55,61,62,87,90,98,101,125,132,135,141,145,159,163,164,220 | sol | view |
| 155 | 25 | 527 | 11,12,13,14,19,30,41,47,50,52,59,68,71,81,94,97,107,132,147,151,155,169,175,183,197 | sol | view |
| 156 | 25 | 528 | 2,9,15,17,27,29,31,32,33,36,47,49,50,60,62,69,77,123,127,128,132,141,150,255,273 | sol | view |
| 157 | 25 | 529 | 9,12,20,21,33,35,37,39,54,55,61,62,87,90,98,101,125,132,140,141,145,159,163,169,225 | sol | view |
| 158 | 25 | 531 | 6,9,10,17,19,24,29,31,39,40,67,68,71,84,101,102,105,118,151,153,159,165,171,195,207 | sol | view |
| 159 | 25 | 532 | 16,18,26,27,33,39,41,50,51,55,69,71,84,87,91,94,132,133,141,143,164,168,169,173,195 | sol | view |
| 160 | 25 | 534 | 11,13,15,17,18,27,38,44,49,52,60,61,68,81,87,94,107,135,149,153,159,171,174,189,210 | sol | view |
| 161 | 25 | 535 | 2,8,26,27,36,41,45,57,62,77,88,95,97,99,101,102,109,114,117,118,141,147,168,192,226 | sol | view |
| 162 | 25 | 536 | 1,8,21,30,31,32,33,41,44,46,49,55,57,61,84,91,113,134,137,139,150,155,176,205,247 | sol | view |
| 163 | 25 | 536 | 3,5,9,11,12,21,24,27,30,44,45,50,54,55,57,63,95,117,123,134,140,145,156,257,279 | sol | view |
| 164 | 25 | 540 | 1,7,8,9,10,14,19,34,36,51,58,69,81,83,97,109,111,115,136,149,152,167,183,208,221 | sol | view |
| 165 | 25 | 540 | 6,13,15,25,28,36,43,47,55,57,58,59,60,65,82,89,91,107,124,127,144,163,183,233,250 | sol | view |
| 166 | 25 | 540 | 8,9,10,11,16,30,36,38,45,55,57,65,68,81,84,95,98,100,116,117,126,135,144,261,279 | sol | view |
| 167 | 25 | 540 | 8,9,10,11,16,30,36,38,45,55,57,65,68,81,84,95,98,100,116,117,126,135,144,261,279 | sol | view |
| 168 | 25 | 540 | 4,6,9,10,17,21,23,25,31,33,36,38,45,50,81,83,115,117,126,133,135,144,146,261,279 | sol | view |
| 169 | 25 | 540 | 4,6,9,10,17,21,23,25,31,33,36,38,45,50,81,83,115,117,126,133,135,144,146,261,279 | sol | view |
| 170 | 25 | 541 | 3,4,11,13,16,17,21,25,26,44,46,64,75,86,87,97,106,109,133,141,165,185,191,215,217 | sol | view |
| 171 | 25 | 541 | 3,5,27,32,33,37,47,50,53,56,57,69,71,78,97,98,109,111,126,144,165,169,183,189,232 | sol | view |
| 172 | 25 | 544 | 1,7,24,26,33,35,40,45,47,51,55,69,87,90,93,96,117,125,134,145,147,184,198,199,200 | sol | view |
| 173 | 25 | 544 | 6,8,20,21,23,41,42,48,59,61,77,80,81,85,90,92,93,102,115,132,139,168,198,207,244 | sol | view |
| 174 | 25 | 547 | 3,5,16,22,26,27,35,47,49,59,67,71,72,85,87,102,103,111,137,144,150,197,200,203,207 | sol | view |
| 175 | 25 | 549 | 4,10,14,24,26,31,34,36,38,40,43,48,59,63,74,89,97,105,117,124,136,152,156,241,308 | sol | view |
| 176 | 25 | 550 | 1,2,5,13,19,20,25,30,39,43,58,59,73,75,76,90,95,103,116,128,130,132,172,262,288 | sol | view |
| 177 | 25 | 550 | 1,11,16,23,24,27,29,36,41,43,44,47,59,70,71,80,99,103,111,116,128,156,167,227,323 | sol | view |
| 178 | 25 | 551 | 3,5,24,25,26,30,35,36,39,40,42,57,68,76,94,109,120,128,152,162,166,175,176,200,223 | sol | view |
| 179 | 25 | 552 | 5,17,18,22,25,27,32,33,39,59,62,87,91,100,102,111,112,135,137,149,165,168,183,201,204 | sol | view |
| 180 | 25 | 552 | 1,3,4,7,8,9,10,15,18,19,21,41,52,54,73,93,95,123,125,136,138,153,168,261,291 | sol | view |
| 181 | 25 | 556 | 6,8,10,13,19,25,32,37,49,54,58,76,84,91,92,100,107,128,145,156,165,185,195,205,206 | sol | view |
| 182 | 25 | 556 | 3,12,13,15,19,23,27,34,35,39,42,45,48,52,53,87,140,145,158,166,171,184,189,201,227 | sol | view |
| 183 | 25 | 556 | 3,12,13,15,19,23,27,34,35,39,42,45,48,52,53,87,140,145,158,166,171,184,189,201,227 | sol | view |
| 184 | 25 | 556 | 1,5,7,8,9,10,12,14,20,27,31,43,47,50,74,93,97,121,125,139,143,153,167,264,292 | sol | view |
| 185 | 25 | 562 | 2,3,5,8,13,19,20,29,33,47,53,54,64,65,76,93,119,123,142,157,161,180,184,221,259 | sol | view |
| 186 | 25 | 570 | 3,9,10,33,36,38,40,42,50,51,60,69,72,75,77,90,113,140,141,151,152,189,200,229,230 | sol | view |
| 187 | 25 | 575 | 4,6,14,16,31,39,63,69,74,81,88,103,107,111,115,120,131,132,133,147,156,159,164,198,218 | sol | view |
| 188 | 25 | 576 | 1,4,9,11,15,19,22,34,36,53,60,76,82,84,104,126,127,128,153,156,165,174,183,219,237 | sol | view |
| 189 | 25 | 576 | 8,9,10,11,16,30,36,38,45,55,57,65,68,81,84,95,98,100,116,135,144,153,162,279,297 | sol | view |
| 190 | 25 | 576 | 4,6,9,10,17,21,23,25,31,33,36,38,45,50,81,83,115,133,135,144,146,153,162,279,297 | sol | view |
| 191 | 25 | 580 | 2,5,7,10,12,13,19,21,22,29,36,40,61,65,74,101,135,139,161,179,183,192,205,209,236 | sol | view |
| 192 | 25 | 580 | 5,6,11,13,16,17,21,25,34,44,54,68,80,88,100,112,120,135,142,145,170,173,195,215,265 | sol | view |
| 193 | 25 | 580 | 11,12,16,17,29,32,39,41,53,55,59,60,68,70,81,84,92,124,125,128,129,156,171,280,300 | sol | view |
| 194 | 25 | 593 | 13,14,15,35,48,51,55,67,73,79,83,91,94,105,109,116,119,124,133,150,171,173,196,217,226 | sol | view |
| 195 | 25 | 595 | 4,13,18,19,22,35,40,48,58,61,62,77,78,82,83,86,118,149,163,168,187,192,202,206,240 | sol | view |
| 196 | 25 | 601 | 7,8,25,34,41,42,46,48,54,55,62,70,71,74,98,103,116,143,168,169,190,192,193,218,240 | sol | view |
| 197 | 25 | 603 | 7,11,12,14,21,25,32,40,52,56,60,67,68,81,91,92,132,144,149,163,177,191,196,235,263 | sol | view |
| 198 | 25 | 603 | 13,23,26,27,35,44,45,49,53,54,57,66,75,99,101,110,122,126,144,158,175,180,189,234,270 | sol | view |
| 199 | 25 | 607 | 6,8,10,13,19,25,32,37,49,54,58,76,84,91,92,100,107,128,156,185,196,205,206,216,246 | sol | view |
| 200 | 25 | 609 | 9,14,15,17,32,45,47,58,67,74,76,79,80,83,97,111,125,126,150,170,186,188,215,224,235 | sol | view |
| 201 | 25 | 611 | 1,10,22,26,32,41,45,54,57,61,62,66,85,86,87,95,97,101,119,132,136,167,176,268,343 | sol | view |
| 202 | 25 | 614 | 15,22,24,31,33,49,53,54,57,60,63,68,74,81,83,104,109,151,155,163,167,217,229,230,234 | sol | view |
| 203 | 25 | 634 | 15,17,24,26,33,43,44,54,57,60,63,73,79,81,88,109,119,160,161,172,173,227,234,235,239 | sol | view |
| 204 | 25 | 643 | 2,9,21,29,38,40,41,42,58,62,67,76,82,83,85,96,104,166,172,186,192,201,207,250,270 | sol | view |
| 205 | 25 | 644 | 7,9,13,18,19,22,31,49,53,61,66,68,71,87,93,94,119,164,178,192,199,206,227,239,253 | sol | view |
| 206 | 25 | 655 | 10,14,15,21,25,26,31,40,51,53,54,57,65,83,84,86,151,152,173,193,194,215,216,246,288 | sol | view |
| 207 | 25 | 661 | 5,7,17,18,23,31,36,38,41,64,73,77,83,84,102,106,111,161,175,196,203,210,238,248,262 | sol | view |
For each squared square instance, the graphical view shows:
left branch: the status just after the last node on the leftmost branch of the search tree,
trashing: the status at the first node of the search tree where trashing occurs (i.e. trashing occurs at a given node if we do not immediately fail at this node but we immediately fail on all children of that node).
Within the context of root and trashing, each graphical view from left to right consists of:
A two-dimensional view, which displays the compulsory part of the squares. In this context a square has a compulsory part if it has a compulsory part on both dimensions. Completely fixed squares are coloured in light grey or white, while not completely fixed squares are coloured in light red.
A cumulative view on the first dimension, which displays the squares that have a compulsory part with respect to the first dimension. Yellow squares correspond to squares that have a compulsory part in the first dimension but no compulsory part in the second dimension. All squares that are below the fat yellow profile correspond to squares for which the origin in the first dimension is fixed.
A cumulative view on the second dimension, which displays the squares that have a compulsory part with respect to the second dimension. Orange squares correspond to squares that have a compulsory part in the second dimension but no compulsory part in the first dimension. All squares that are below the fat orange profile correspond to squares for which the origin in the second dimension is fixed.
Within the context of left branch, each graphical view consists of similar graphic views. The only difference is that these views show how the compulsory part of an object increases as we go down a branch of the search tree. In this context the additional part of the compulsory part of an object is coloured in lighter blue as we go down a branch. This allows to see how the compulsory part of an object increases along a branch of the search tree. Finally not fat profile is shown in this context since we would have too many of them (i.e., one for each node of the path).
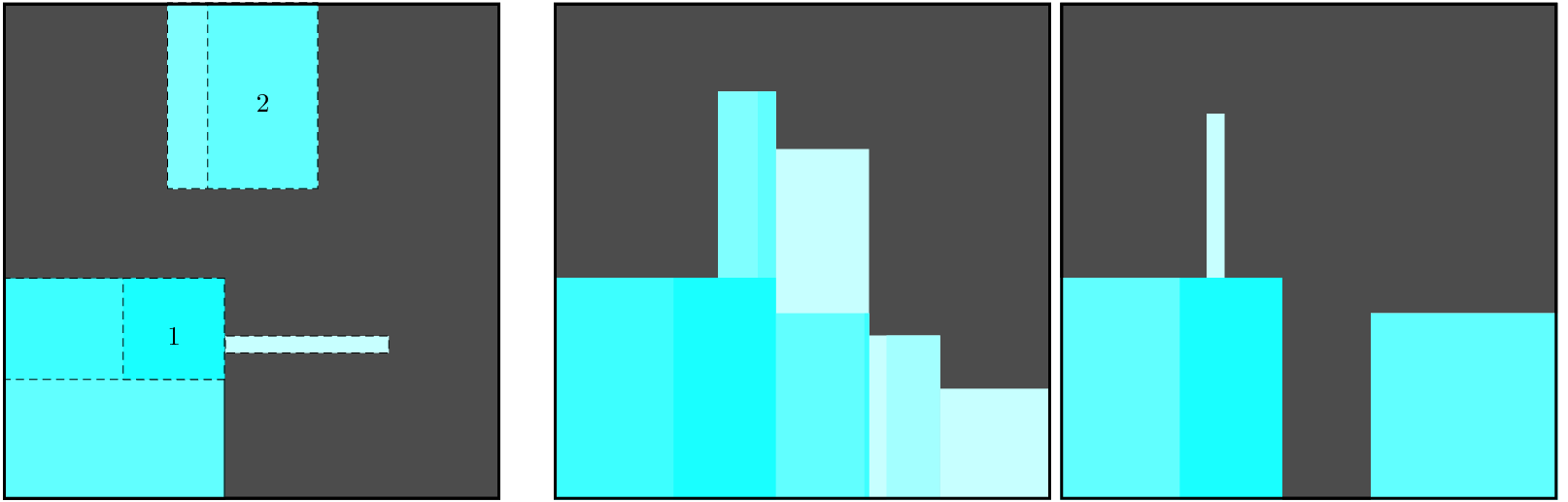
Let us comment the view associated with the first instance of the squared squares problems:
In the context of root, the biggest square (i.e., the light red square labelled with a 1) has a compulsory part thanks to the symmetry constraint. It also has a compulsory part with respect to the first dimension (note that we draw a rectangle since we consider the full height of the corresponding square). Finally it also has a compulsory part with respect to the second dimension.
Figure 3.7.72. the root view for instance squared_squares_001

In the context of trashing, the biggest square (i.e., the white square labelled with a 1) is completely fixed at the lower leftmost corner of the placement space. The second biggest square (i.e., the light red square labelled with a 2) is not completely fixed but has a compulsory part in both dimensions. Finally a third square has a tiny compulsory part. We retrieve these three squares in the cumulative views associated with the first and second dimension. Finally, within the cumulative view associated with the first dimension we also have a yellow square labelled with 8, which corresponds to a square that only has a compulsory part in the first dimension. On the one hand, the fat yellow profile corresponding to the first dimension consists of the three squares 1, 3, 8, which are completely fixed with respect to the first dimension. On the other hand the fat orange profile corresponding to the second dimension consists of the two squares 1 and 2.
Figure 3.7.73. the trashing view for instance squared_squares_001
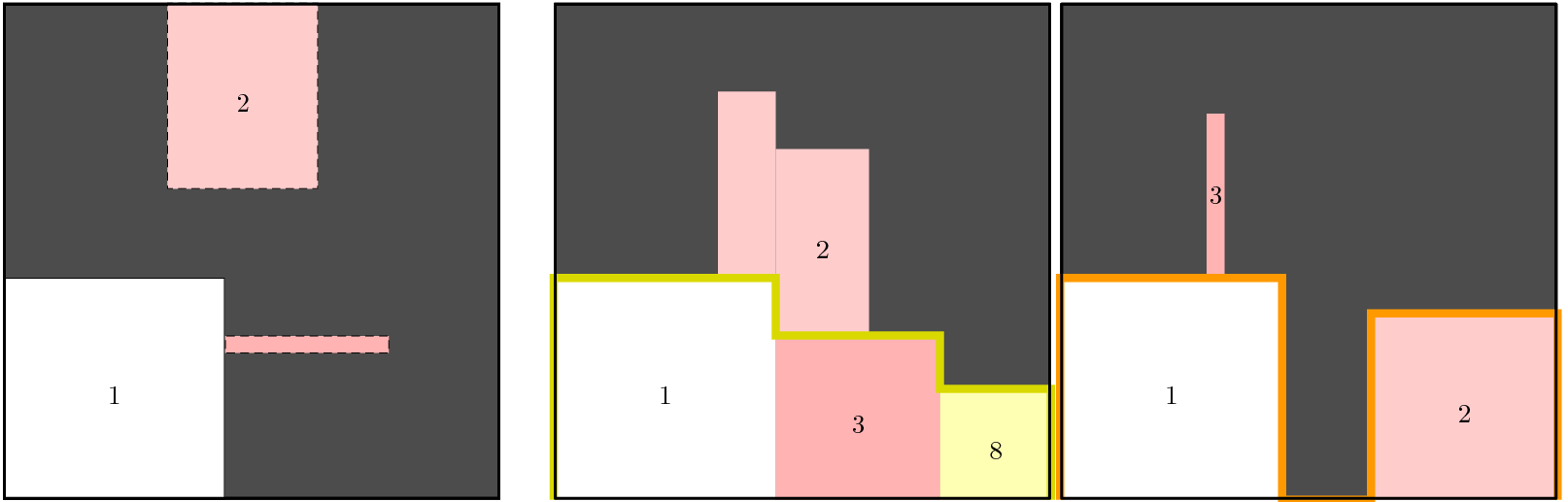
In the context of left branch, we can observe how the compulsory part grows as we go down the leftmost branch of the search tree. For instance at the root node we have a small compulsory part for the biggest square (i.e., the square labelled by 1). Then, as we go down the leftmost branch, this compulsory part gradually increases until the square becomes completely fixed in the next two steps. We can also observe that the heuristics tends to gradually create compulsory parts on the cumulative view associated with the first dimension (in light blue on the second picture).
Figure 3.7.74. the left branch view for instance squared_squares_001