Global Constraint Catalog

3.5. Constraints argument patterns

If you do not know the name of the global constraint you are looking for, but you know the types of its arguments this section allows to find out all global constraints which have similar arguments. For this purpose we associate to each global constraint of the catalogue a unique normalised signature tree derived from the types of its arguments.An informal rule used in the catalogue about the order of the arguments of a constraint is that we usually first mention a domain variable which represents a result computed from one or several collections that occur just after. Finally, eventual parameters are put as the last arguments of the constraint. The purpose of this normalised signature tree is to get a concise normal form of the arguments of a global constraint that does not depend of the order in which these arguments are defined.

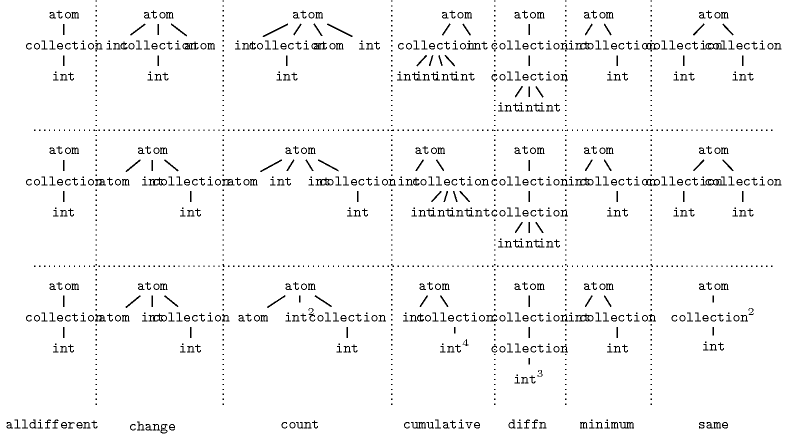
Figure 3.5.1. Illustrating steps (2), (3) and (4) for computing the normalised signature tree

The normalisation takes as input the slots Type(s) and Argument(s) of the description of a global constraintSee Section 2.2.4 for the description of these slots. and computes the normalised signature tree in four steps:

The first step converts all types related to variables to their corresponding ground counterparts: the types $𝚍𝚟𝚊𝚛$ , $𝚜𝚟𝚊𝚛$ , $𝚖𝚟𝚊𝚛$ and $𝚛𝚟𝚊𝚛$ are respectively transformed to $𝚒𝚗𝚝$ , $𝚜𝚒𝚗𝚝$ , $𝚖𝚒𝚗𝚝$ and $𝚛𝚎𝚊𝚕$ .
The second step builds a tree of types $𝒯$ by exploring the slot Argument(s) and by developing the compound data types possibly used. The root of this tree is the type $𝚊𝚝𝚘𝚖$ and represents the name of the global constraint.
The third step normalises the tree of types $𝒯$ by first normalising each subtree of $𝒯$ and then by sorting the children of $𝒯$ . We assume the following ordering on the different types: $𝚊𝚝𝚘𝚖 ≺ 𝚒𝚗𝚝 ≺ 𝚜𝚒𝚗𝚝 ≺ 𝚖𝚒𝚗𝚝 ≺ 𝚛𝚎𝚊𝚕 ≺ 𝚕𝚒𝚜𝚝 ≺ 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗$ . Let $𝒯_{n}$ denote the normalised tree obtained at this third step.
Finally the last step tries to reduce the size of the normalised tree $𝒯_{n}$ by identifying $k (k > 1)$ children of a vertex $v$ of $𝒯_{n}$ for which the $k$ subtrees are identical. When such a configuration is identified the $k$ subtrees of $v$ are replaced by a single subtree and the integer $k$ is put as an exponent of $v$ .

**Table 3.5.1.** Example of information associated with a normalised signature tree (within the signature tree $𝚌𝚘𝚕$ is a shortcut for $𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗$ )
	$𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚘𝚗_𝚒𝚗𝚝𝚎𝚛𝚜𝚎𝚌𝚝𝚒𝚘𝚗$ $𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚐𝚛𝚘𝚞𝚙𝚜_𝚘𝚏_𝚘𝚗𝚎𝚜$ $𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝$ $𝚒𝚗𝚌𝚘𝚖𝚙𝚊𝚛𝚊𝚋𝚕𝚎$ $𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎_𝚌𝚑𝚊𝚒𝚗$ $𝚒𝚗𝚟𝚎𝚛𝚜𝚎_𝚠𝚒𝚝𝚑𝚒𝚗_𝚛𝚊𝚗𝚐𝚎$ $𝚕𝚎𝚡_𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ $𝚕𝚎𝚡_𝚎𝚚𝚞𝚊𝚕$ $𝚕𝚎𝚡_𝚐𝚛𝚎𝚊𝚝𝚎𝚛$ $𝚕𝚎𝚡_𝚐𝚛𝚎𝚊𝚝𝚎𝚛𝚎𝚚$ $𝚕𝚎𝚡_𝚕𝚎𝚜𝚜$ $𝚕𝚎𝚡_𝚕𝚎𝚜𝚜𝚎𝚚$ $𝚕𝚎𝚡_𝚕𝚎𝚜𝚜𝚎𝚚_𝚊𝚕𝚕𝚙𝚎𝚛𝚖$ $𝚜𝚊𝚖𝚎$ $𝚜𝚊𝚖𝚎_𝚒𝚗𝚝𝚎𝚛𝚜𝚎𝚌𝚝𝚒𝚘𝚗$ $𝚜𝚘𝚛𝚝$ $𝚞𝚜𝚎𝚍_𝚋𝚢$ $𝚞𝚜𝚎𝚜$ $𝚟𝚎𝚌_𝚎𝚚_𝚝𝚞𝚙𝚕𝚎$

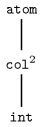
The three rows of Figure 3.5.1 illustrate respectively the second, third and fourth steps for computing the normalised signature tree associated with the arguments of the constraints $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ , $𝚌𝚑𝚊𝚗𝚐𝚎$ , $𝚌𝚘𝚞𝚗𝚝$ , $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ , $𝚍𝚒𝚏𝚏𝚗$ , $𝚖𝚒𝚗𝚒𝚖𝚞𝚖$ and $𝚜𝚊𝚖𝚎$ .

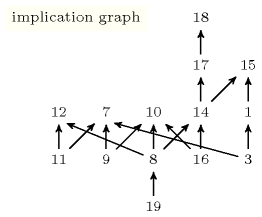
The next sections provide for each possible constraints arity all existing normalised signature trees together with the corresponding list of global constraints of the catalogue. The leftmost part of an entry corresponds to a normalised signature tree, while the rightmost upper part gives the corresponding list of global constraints. Finally the rightmost lower part describes the dependency between the constraints of the list: there is an edge from a constraint ${𝚌𝚝𝚛}_{1}$ to a constraint ${𝚌𝚝𝚛}_{2}$ if and only if the fact that ${𝚌𝚝𝚛}_{1}$ holds implies that ${𝚌𝚝𝚛}_{2}$ also holds. For instance, consider the constraints associated with the normalised signature tree corresponding to two collections of integers depicted by Table 3.5.1. There is an edge from 16 (i.e., $𝚜𝚘𝚛𝚝$ ) to 14 (i.e., $𝚜𝚊𝚖𝚎$ ) since the fact that a $𝚜𝚘𝚛𝚝$ constraint holds implies that a $𝚜𝚊𝚖𝚎$ constraint also holds.

Global Constraint Catalog

3. Description of the Catalogue

3.5. Constraints argument patterns

Figure 3.5.1. Illustrating steps (2), (3) and (4) for computing the normalised signature tree

Table 3.5.1. Example of information associated with a normalised signature tree (within the signature tree $𝚌𝚘𝚕$ is a shortcut for $𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗$ )

Global Constraint Catalog

3. Description of the Catalogue

3.5. Constraints argument patterns

Figure 3.5.1. Illustrating steps (2), (3) and (4) for computing the normalised signature tree

Table 3.5.1. Example of information associated with a normalised signature tree (within the signature tree 𝚌𝚘𝚕 is a shortcut for 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗)

Table 3.5.1. Example of information associated with a normalised signature tree (within the signature tree $𝚌𝚘𝚕$ is a shortcut for $𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗$ )