3.7.15. Assigning and scheduling tasks that run in parallel
modelling: assigning and scheduling tasks that run in parallel Consider a set of tasks defined by a set of subtasks, where each subtask has the following attributes:
A start telling when the subtask starts.
A duration giving the duration of the subtask.
A deadline indicating the date by which the subtask must be finished.
A person indicating which person performs the subtask.
Both the start and the person correspond to decision variables, while the duration and the deadline are integers. Since all subtasks of a same task must run in parallel, their starts, durations and deadlines are identical. Since a person can perform at most one task at each timepoint, persons assigned to the subtasks of a same task must all be distinct. We also assume that a subtask cannot be preempted.
As an instance of this pattern, consider the problem of scheduling surgical operations in a hospital. Each surgery corresponds to a task that requires a number of persons with specific skills; these persons will all work together during the operation (e.g., typically an anaesthetist, a surgeon and one or several nurses). Moreover, each person has his own calendar defining his unavailability. On the one hand, let us assume we have two anaesthetists, two surgeons and four nurses, labelled from 1 to 8. Each of them has the following unavailability over the time horizon :
The first anaesthetist is not available during the time periods , , and .
The second anaesthetist is not available during the time periods , , , and .
The first surgeon is not available during the time periods , , and .
The second surgeon is not available during the time periods , and .
The four nurses are all not available during the time periods , , , and .
On the other hand, let us suppose we have to schedule five surgery tasks, each of them requiring a specific team:
Task needs one anaesthetist, one surgeon and two nurses during two consecutive time slots.
Task needs one anaesthetist, one surgeon and one nurse during four consecutive time slots.
Task needs one anaesthetist, two surgeons and two nurses during three consecutive time slots.
Task needs one anaesthetist, one surgeon and three nurses during two consecutive time slots.
Task needs one anaesthetist, one surgeon and one nurse during six consecutive time slots.
Moreover, tasks , , , and must be respectively completed no later than timepoint 12, 15, 24, 24 and 24. The problem is modelled by using a two-dimensional constraint, where the first and second dimensions respectively correspond to the time and resource axes. For each person required by a task we create a rectangle of length corresponding to the necessary duration and of height 1 (since it requires one person). The coordinates of the lower left point of the rectangle correspond to the start of the corresponding task as well as to the person that will be assigned to the subtask (i.e., a value between 1 and 2 for an anaesthetist, a value between 3 and 4 for a surgeon, and a value between 5 and 8 for a nurse). Both the start and the person correspond to a domain variable. Each unavailability period of an anaesthetist, a surgeon and a nurse is modelled by introducing a fixed rectangle (i.e., its coordinates are set to the start of the unavailability period and to the person to which the unavailability belongs; its duration is set to the duration of the unavailability period) that prevent tasks overlapping the corresponding time period for a specific person. This leads to the following constraint,
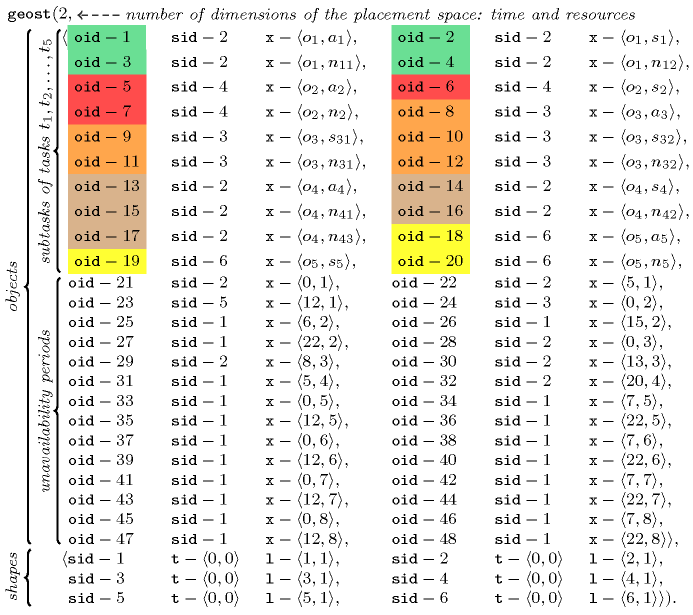
Figure 3.7.1. A solution to the surgery scheduling problem using four nurses where the start and the latest completion time of each task are respectively shown in bold and in red; a solution using only 3 nurses can be obtained by starting task at instant 13 and by assigning it to the second anaesthetist rather than to the first one.
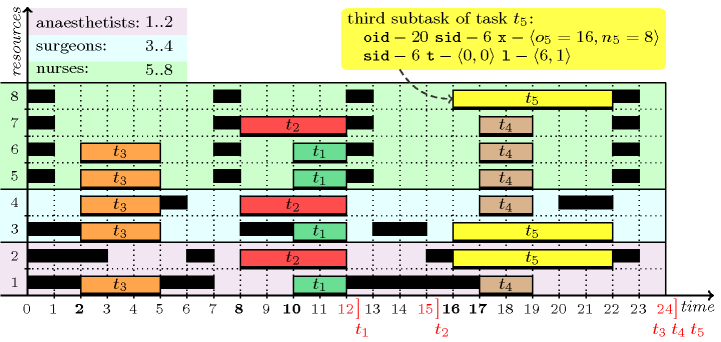
A deadline constraint for a surgery starting at and of duration is modelled by a precedence constraint of the form . This leads to the five constraints , , , , and . Finally, we break symmetry on the assignment variables corresponding to a group of similar persons. In the example, the four nurses are similar since (1) they all have exactly the same unavailability periods, and since (2) no task requires a specific nurse. For each task using more than one nurse (i.e., tasks , , and ) this leads to a chain of strict inequalities, i.e., , , and . Figure 3.7.1 depicts a solution to the problem corresponding to the assignment
The entry corresponding to the keyword relaxation dimension shows how to express relaxation in the context of over-constrained problems where we have too many surgeries to schedule with respect to the number of anaesthetists, surgeons and nurses and to their unavailability periods.