3.7.236. Smallest square for packing rectangles with distinct sizes

Denotes that a constraint can be used for finding the smallest square where one can pack n rectangles for which all the 2·n sizes are distinct integer values. The problem is described in http://www.stetson.edu/~efriedma/mathmagic/0899.html. Figures 3.7.68, 3.7.69 and 3.7.70 present the smallest square (not necessarily optimal) found with 𝚐𝚎𝚘𝚜𝚝 for respectively placing 9, 10, 11, 12, 13 and 14 rectangles of distinct sizes.

Figure 3.7.68. (Left) Tiling a square of size 24 with 9 rectangles of distinct sizes 1×18, 17×2, 15×3, 4×14, 16×5, 12×6, 7×13, 10×8, 9×11; (Right) Tiling a square of size 28 with 10 rectangles of distinct sizes 1×20, 2×19, 18×3, 4×17, 5×16, 6×15, 7×14, 12×8, 9×13, 10×11.
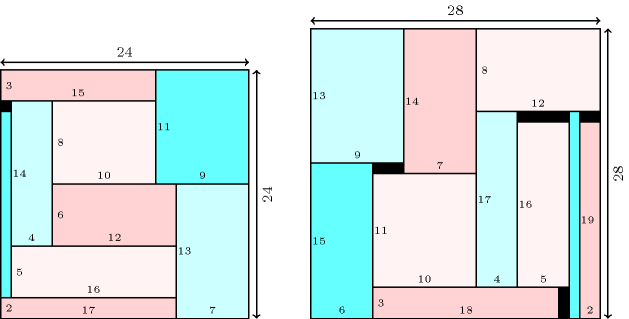
ctrs/preface-209-tikz
Figure 3.7.69. (Left) Tiling a square of size 32 with 11 rectangles of distinct sizes 1×22, 21×2, 3×20, 18×4, 19×5, 16×6, 7×17, 8×15, 14×9, 13×10, 12×11; (Right) Tiling a square of size 37 with 12 rectangles of distinct sizes 1×24, 2×23, 3×22, 4×21, 5×20, 6×19, 7×18, 8×17, 9×16, 15×10, 11×14, 12×13.
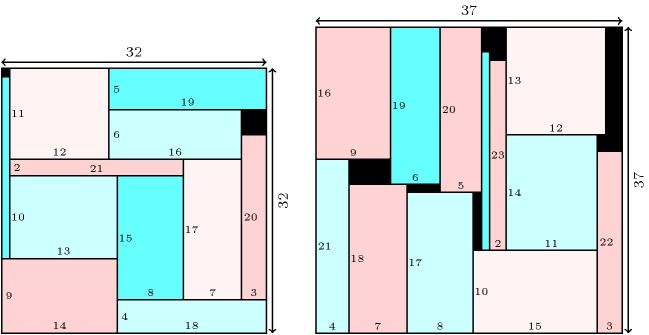
ctrs/preface-210-tikz
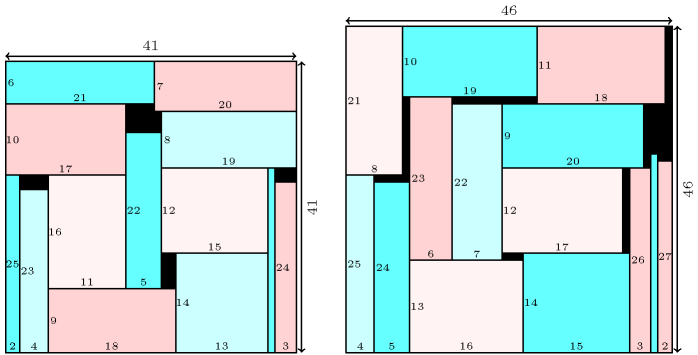
Figure 3.7.70. (Left) Tiling a square of size 41 with 13 rectangles of distinct sizes 1×26, 2×25, 3×24, 4×23, 5×22, 21×6, 20×7, 19×8, 18×9, 17×10, 11×16, 15×12, 13×14; (Right) Tiling a square of size 46 with 14 rectangles of distinct sizes 1×28, 2×27, 3×26, 4×25, 5×24, 6×23, 7×22, 8×21, 20×9, 19×10, 18×11, 17×12, 16×13, 15×14.
ctrs/preface-211-tikz