Global Constraint Catalog: Catmost

5.42. atmost_nvector

DESCRIPTION

LINKS

GRAPH

Origin

Derived from $𝚗𝚟𝚎𝚌𝚝𝚘𝚛$

Constraint

$𝚊𝚝𝚖𝚘𝚜𝚝_𝚗𝚟𝚎𝚌𝚝𝚘𝚛 (𝙽𝚅𝙴𝙲, 𝚅𝙴𝙲𝚃𝙾𝚁𝚂)$

Type

𝚅𝙴𝙲𝚃𝙾𝚁

𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)

Arguments

$𝙽𝚅𝙴𝙲$	$𝚍𝚟𝚊𝚛$
$𝚅𝙴𝙲𝚃𝙾𝚁𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚎𝚌 - 𝚅𝙴𝙲𝚃𝙾𝚁)$

Restrictions

| 𝚅𝙴𝙲𝚃𝙾𝚁 | \geq 1

𝙽𝚅𝙴𝙲 \geq 𝚖𝚒𝚗 (1, | 𝚅𝙴𝙲𝚃𝙾𝚁𝚂 |)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙴𝙲𝚃𝙾𝚁𝚂, 𝚟𝚎𝚌)

𝚜𝚊𝚖𝚎_𝚜𝚒𝚣𝚎

(𝚅𝙴𝙲𝚃𝙾𝚁𝚂, 𝚟𝚎𝚌)

Purpose

The number of distinct tuples of values taken by the vectors of the collection $𝚅𝙴𝙲𝚃𝙾𝚁𝚂$ is less than or equal to $𝙽𝚅𝙴𝙲$ . Two tuples of values $〈 A_{1}, A_{2}, \dots, A_{m} 〉$ and $〈 B_{1}, B_{2}, \dots, B_{m} 〉$ are $d i s t i n c t$ if and only if there exist an integer $i \in [1, m]$ such that $A_{i} \neq B_{i}$ .

Example

(\begin{matrix} 3, 〈\begin{matrix} 𝚟𝚎𝚌 - 〈5, 6〉, \\ 𝚟𝚎𝚌 - 〈5, 6〉, \\ 𝚟𝚎𝚌 - 〈9, 3〉, \\ 𝚟𝚎𝚌 - 〈5, 6〉, \\ 𝚟𝚎𝚌 - 〈9, 3〉 \end{matrix}〉 \end{matrix})

The $𝚊𝚝𝚖𝚘𝚜𝚝_𝚗𝚟𝚎𝚌𝚝𝚘𝚛$ constraint holds since the collection $𝚅𝙴𝙲𝚃𝙾𝚁𝚂$ involves at most 3 distinct tuples of values (i.e., in fact the 2 distinct tuples $〈 5, 6 〉$ and $〈 9, 3 〉$ ).

Typical

| 𝚅𝙴𝙲𝚃𝙾𝚁 | > 1

𝙽𝚅𝙴𝙲 > 1

𝙽𝚅𝙴𝙲 < | 𝚅𝙴𝙲𝚃𝙾𝚁𝚂 |

| 𝚅𝙴𝙲𝚃𝙾𝚁𝚂 | > 1

Symmetries

$𝙽𝚅𝙴𝙲$ can be increased.
Items of $𝚅𝙴𝙲𝚃𝙾𝚁𝚂$ are permutable.
Items of $𝚅𝙴𝙲𝚃𝙾𝚁𝚂 . 𝚟𝚎𝚌$ are permutable (same permutation used).
All occurrences of two distinct tuples of values of $𝚅𝙴𝙲𝚃𝙾𝚁𝚂 . 𝚟𝚎𝚌$ can be swapped; all occurrences of a tuple of values of $𝚅𝙴𝙲𝚃𝙾𝚁𝚂 . 𝚟𝚎𝚌$ can be renamed to any unused tuple of values.

Arg. properties

Contractible wrt. $𝚅𝙴𝙲𝚃𝙾𝚁𝚂$ .

Reformulation

By introducing an extra variable $𝙽𝚅 \in [0, | 𝚅𝙴𝙲𝚃𝙾𝚁𝚂 |]$ , the $𝚊𝚝𝚖𝚘𝚜𝚝_𝚗𝚟𝚎𝚌𝚝𝚘𝚛$ $(𝙽𝚅, 𝚅𝙴𝙲𝚃𝙾𝚁𝚂)$ constraint can be expressed in term of an $𝚗𝚟𝚎𝚌𝚝𝚘𝚛$ $(𝙽𝚅, 𝚅𝙴𝙲𝚃𝙾𝚁𝚂)$ constraint and of an inequality constraint $𝙽𝚅 \leq 𝙽𝚅𝙴𝙲$ .

implied by: $𝚗𝚟𝚎𝚌𝚝𝚘𝚛$ ( $\leq$ $𝙽𝚅𝙴𝙲$ replaced by $=$ $𝙽𝚅𝙴𝙲$ ), $𝚘𝚛𝚍𝚎𝚛𝚎𝚍_𝚊𝚝𝚖𝚘𝚜𝚝_𝚗𝚟𝚎𝚌𝚝𝚘𝚛$ .

used in graph description: $𝚕𝚎𝚡_𝚎𝚚𝚞𝚊𝚕$ .

Keywords

characteristic of a constraint: vector.

constraint type: counting constraint, value partitioning constraint.

final graph structure: strongly connected component, equivalence.

modelling: number of distinct equivalence classes.

problems: domination.

Arc input(s)

$𝚅𝙴𝙲𝚃𝙾𝚁𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚎𝚌𝚝𝚘𝚛𝚜 1, 𝚟𝚎𝚌𝚝𝚘𝚛𝚜 2)

Arc arity

Arc constraint(s)

𝚕𝚎𝚡_𝚎𝚚𝚞𝚊𝚕

(𝚟𝚎𝚌𝚝𝚘𝚛𝚜 1 . 𝚟𝚎𝚌, 𝚟𝚎𝚌𝚝𝚘𝚛𝚜 2 . 𝚟𝚎𝚌)

Graph property(ies)

𝐍𝐒𝐂𝐂

\leq 𝙽𝚅𝙴𝙲

Graph class

𝙴𝚀𝚄𝙸𝚅𝙰𝙻𝙴𝙽𝙲𝙴

Graph model

Parts (A) and (B) of Figure 5.42.1 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐒𝐂𝐂$ graph property we show the different strongly connected components of the final graph. Each strongly connected component corresponds to a tuple of values that is assigned to some vectors of the $𝚅𝙴𝙲𝚃𝙾𝚁𝚂$ collection. The 2 following tuple of values $〈 5, 6 〉$ and $〈 9, 3 〉$ are used by the vectors of the $𝚅𝙴𝙲𝚃𝙾𝚁𝚂$ collection.

Figure 5.42.1. Initial and final graph of the $𝚊𝚝𝚖𝚘𝚜𝚝_𝚗𝚟𝚎𝚌𝚝𝚘𝚛$ constraint


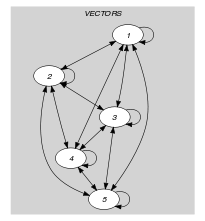
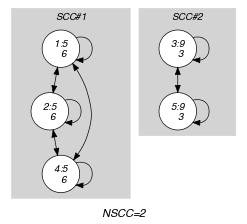
(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.42. atmost_nvector

Figure 5.42.1. Initial and final graph of the 𝚊𝚝𝚖𝚘𝚜𝚝_𝚗𝚟𝚎𝚌𝚝𝚘𝚛 constraint

Figure 5.42.1. Initial and final graph of the $𝚊𝚝𝚖𝚘𝚜𝚝_𝚗𝚟𝚎𝚌𝚝𝚘𝚛$ constraint