Global Constraint Catalog: Clex_chain

5.225. lex_chain_less

DESCRIPTION

LINKS

GRAPH

Origin

[BeldiceanuCarlsson02c]

Constraint

$𝚕𝚎𝚡_𝚌𝚑𝚊𝚒𝚗_𝚕𝚎𝚜𝚜 (𝚅𝙴𝙲𝚃𝙾𝚁𝚂)$

Usual name

$𝚕𝚎𝚡_𝚌𝚑𝚊𝚒𝚗$

Type

𝚅𝙴𝙲𝚃𝙾𝚁

𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)

Argument

𝚅𝙴𝙲𝚃𝙾𝚁𝚂

𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚎𝚌 - 𝚅𝙴𝙲𝚃𝙾𝚁)

Restrictions

| 𝚅𝙴𝙲𝚃𝙾𝚁 | \geq 1

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙴𝙲𝚃𝙾𝚁, 𝚟𝚊𝚛)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙴𝙲𝚃𝙾𝚁𝚂, 𝚟𝚎𝚌)

𝚜𝚊𝚖𝚎_𝚜𝚒𝚣𝚎

(𝚅𝙴𝙲𝚃𝙾𝚁𝚂, 𝚟𝚎𝚌)

Purpose

For each pair of consecutive vectors ${𝚅𝙴𝙲𝚃𝙾𝚁}_{i}$ and ${𝚅𝙴𝙲𝚃𝙾𝚁}_{i + 1}$ of the $𝚅𝙴𝙲𝚃𝙾𝚁𝚂$ collection we have that ${𝚅𝙴𝙲𝚃𝙾𝚁}_{i}$ is lexicographically strictly less than ${𝚅𝙴𝙲𝚃𝙾𝚁}_{i + 1}$ . Given two vectors, $\vec{X}$ and $\vec{Y}$ of $n$ components, $〈 X_{0}, \dots, X_{n - 1} 〉$ and $〈 Y_{0}, \dots, Y_{n - 1} 〉$ , $\vec{X}$ is lexicographically strictly less than $\vec{Y}$ if and only if $X_{0} < Y_{0}$ or $X_{0} = Y_{0}$ and $〈 X_{1}, \dots, X_{n - 1} 〉$ is lexicographically strictly less than $〈 Y_{1}, \dots, Y_{n - 1} 〉$ .

Example

(〈𝚟𝚎𝚌 - 〈5, 2, 3, 9〉, 𝚟𝚎𝚌 - 〈5, 2, 6, 2〉, 𝚟𝚎𝚌 - 〈5, 2, 6, 3〉〉)

The $𝚕𝚎𝚡_𝚌𝚑𝚊𝚒𝚗_𝚕𝚎𝚜𝚜$ constraint holds since:

The first vector $〈 5, 2, 3, 9 〉$ of the $𝚅𝙴𝙲𝚃𝙾𝚁𝚂$ collection is lexicographically strictly less than the second vector $〈 5, 2, 6, 2 〉$ of the $𝚅𝙴𝙲𝚃𝙾𝚁𝚂$ collection.
The second vector $〈 5, 2, 6, 2 〉$ of the $𝚅𝙴𝙲𝚃𝙾𝚁𝚂$ collection is lexicographically strictly less than the third vector $〈 5, 2, 6, 3 〉$ of the $𝚅𝙴𝙲𝚃𝙾𝚁𝚂$ collection.

Typical

| 𝚅𝙴𝙲𝚃𝙾𝚁 | > 1

| 𝚅𝙴𝙲𝚃𝙾𝚁𝚂 | > 1

Arg. properties

Contractible wrt. $𝚅𝙴𝙲𝚃𝙾𝚁𝚂$ .
Suffix-extensible wrt. $𝚅𝙴𝙲𝚃𝙾𝚁𝚂 . 𝚟𝚎𝚌$ (add items at same position).

Usage

This constraint was motivated for breaking symmetry: more precisely when one wants to lexicographically order the consecutive columns of a matrix of decision variables. A further motivation is that using a set of lexicographic ordering constraints between two vectors does usually not allows to come up with a complete pruning.

Algorithm

A filtering algorithm achieving arc-consistency for a chain of lexicographical ordering constraints is presented in [BeldiceanuCarlsson02c].

Six different ways of integrating a chain of lexicographical ordering constraints within non-overlapping constraints like $𝚍𝚒𝚏𝚏𝚗$ or $𝚐𝚎𝚘𝚜𝚝$ and within their corresponding necessary condition like the $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ constraint are shown in [AgrenCarlssonBeldiceanuSbihiTruchetZampelli09].

Systems

lexChain in Choco, lex_chain in SICStus.

See also

common keyword: $𝚐𝚎𝚘𝚜𝚝$ (symmetry, lexicographic ordering on the origins of $𝚝𝚊𝚜𝚔𝚜$ , $𝚛𝚎𝚌𝚝𝚊𝚗𝚐𝚕𝚎𝚜$ , $...$ ), $𝚕𝚎𝚡_𝚋𝚎𝚝𝚠𝚎𝚎𝚗$ , $𝚕𝚎𝚡_𝚐𝚛𝚎𝚊𝚝𝚎𝚛$ , $𝚕𝚎𝚡_𝚐𝚛𝚎𝚊𝚝𝚎𝚛𝚎𝚚$ , $𝚕𝚎𝚡_𝚕𝚎𝚜𝚜𝚎𝚚$ (lexicographic order).

implied by: $𝚜𝚝𝚛𝚒𝚌𝚝_𝚕𝚎𝚡 2$ .

implies: $𝚕𝚎𝚡_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ , $𝚕𝚎𝚡_𝚌𝚑𝚊𝚒𝚗_𝚕𝚎𝚜𝚜𝚎𝚚$ .

part of system of constraints: $𝚕𝚎𝚡_𝚕𝚎𝚜𝚜$ .

related: $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ , $𝚍𝚒𝚏𝚏𝚗$ (lexicographic ordering on the origins of $𝚝𝚊𝚜𝚔𝚜$ , $𝚛𝚎𝚌𝚝𝚊𝚗𝚐𝚕𝚎𝚜$ , $...$ ).

system of constraints: $𝚜𝚝𝚛𝚒𝚌𝚝_𝚕𝚎𝚡 2$ .

used in graph description: $𝚕𝚎𝚡_𝚕𝚎𝚜𝚜$ .

Keywords

application area: floor planning problem.

characteristic of a constraint: vector.

constraint type: decomposition, order constraint, system of constraints.

filtering: arc-consistency.

heuristics: heuristics and lexicographical ordering.

modelling: degree of diversity of a set of solutions.

modelling exercises: degree of diversity of a set of solutions.

symmetry: symmetry, matrix symmetry, lexicographic order.

Arc input(s)

$𝚅𝙴𝙲𝚃𝙾𝚁𝚂$

Arc generator

𝑃𝐴𝑇𝐻

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚎𝚌𝚝𝚘𝚛𝚜 1, 𝚟𝚎𝚌𝚝𝚘𝚛𝚜 2)

Arc arity

Arc constraint(s)

𝚕𝚎𝚡_𝚕𝚎𝚜𝚜

(𝚟𝚎𝚌𝚝𝚘𝚛𝚜 1 . 𝚟𝚎𝚌, 𝚟𝚎𝚌𝚝𝚘𝚛𝚜 2 . 𝚟𝚎𝚌)

Graph property(ies)

𝐍𝐀𝐑𝐂

= | 𝚅𝙴𝙲𝚃𝙾𝚁𝚂 | - 1

Graph model

Parts (A) and (B) of Figure 5.225.1 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐀𝐑𝐂$ graph property, the arcs of the final graph are stressed in bold. The $𝚕𝚎𝚡_𝚌𝚑𝚊𝚒𝚗_𝚕𝚎𝚜𝚜$ constraint holds since all the arc constraints of the initial graph are satisfied.

Figure 5.225.1. Initial and final graph of the $𝚕𝚎𝚡_𝚌𝚑𝚊𝚒𝚗_𝚕𝚎𝚜𝚜$ constraint


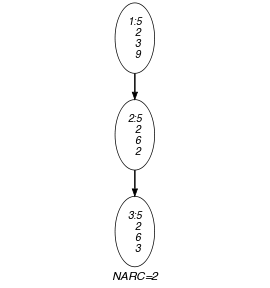
(a)	(b)

Signature

Since we use the $𝑃𝐴𝑇𝐻$ arc generator on the $𝚅𝙴𝙲𝚃𝙾𝚁𝚂$ collection the number of arcs of the initial graph is equal to $| 𝚅𝙴𝙲𝚃𝙾𝚁𝚂 | - 1$ . For this reason we can rewrite $𝐍𝐀𝐑𝐂 = | 𝚅𝙴𝙲𝚃𝙾𝚁𝚂 | - 1$ to $𝐍𝐀𝐑𝐂 \geq | 𝚅𝙴𝙲𝚃𝙾𝚁𝚂 | - 1$ and simplify $\underset{̲}{\bar{𝐍𝐀𝐑𝐂}}$ to $\bar{𝐍𝐀𝐑𝐂}$ .

Global Constraint Catalog

5. Global Constraint Catalogue

5.225. lex_chain_less

Figure 5.225.1. Initial and final graph of the 𝚕𝚎𝚡_𝚌𝚑𝚊𝚒𝚗_𝚕𝚎𝚜𝚜 constraint

Figure 5.225.1. Initial and final graph of the $𝚕𝚎𝚡_𝚌𝚑𝚊𝚒𝚗_𝚕𝚎𝚜𝚜$ constraint