Global Constraint Catalog: Ccoloured

5.73. coloured_cumulative

DESCRIPTION

LINKS

GRAPH

Origin

Derived from $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ and $𝚗𝚟𝚊𝚕𝚞𝚎𝚜$ .

Constraint

$𝚌𝚘𝚕𝚘𝚞𝚛𝚎𝚍_𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎 (𝚃𝙰𝚂𝙺𝚂, 𝙻𝙸𝙼𝙸𝚃)$

Synonym

$𝚌𝚘𝚕𝚘𝚛𝚎𝚍_𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ .

Arguments

$𝚃𝙰𝚂𝙺𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (\begin{matrix} 𝚘𝚛𝚒𝚐𝚒𝚗 - 𝚍𝚟𝚊𝚛, \\ 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 𝚍𝚟𝚊𝚛, \\ 𝚎𝚗𝚍 - 𝚍𝚟𝚊𝚛, \\ 𝚌𝚘𝚕𝚘𝚞𝚛 - 𝚍𝚟𝚊𝚛 \end{matrix})$
$𝙻𝙸𝙼𝙸𝚃$	$𝚒𝚗𝚝$

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎_𝚊𝚝_𝚕𝚎𝚊𝚜𝚝

(2, 𝚃𝙰𝚂𝙺𝚂, [𝚘𝚛𝚒𝚐𝚒𝚗, 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗, 𝚎𝚗𝚍])

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚃𝙰𝚂𝙺𝚂, 𝚌𝚘𝚕𝚘𝚞𝚛)

𝚃𝙰𝚂𝙺𝚂 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 \geq 0

𝚃𝙰𝚂𝙺𝚂 . 𝚘𝚛𝚒𝚐𝚒𝚗 \leq 𝚃𝙰𝚂𝙺𝚂 . 𝚎𝚗𝚍

𝙻𝙸𝙼𝙸𝚃 \geq 0

Purpose

Consider the set $𝒯$ of tasks described by the $𝚃𝙰𝚂𝙺𝚂$ collection. The $𝚌𝚘𝚕𝚘𝚞𝚛𝚎𝚍_𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ constraint forces that, at each point in time, the number of distinct colours of the set of tasks that overlap that point, does not exceed a given limit. A task overlaps a point $i$ if and only if (1) its origin is less than or equal to $i$ , and (2) its end is strictly greater than $i$ . For each task of $𝒯$ it also imposes the constraint $𝚘𝚛𝚒𝚐𝚒𝚗 + 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 = 𝚎𝚗𝚍$ .

Example

(\begin{matrix} 〈\begin{matrix} 𝚘𝚛𝚒𝚐𝚒𝚗 - 1 & 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 2 & 𝚎𝚗𝚍 - 3 & 𝚌𝚘𝚕𝚘𝚞𝚛 - 1, \\ 𝚘𝚛𝚒𝚐𝚒𝚗 - 2 & 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 9 & 𝚎𝚗𝚍 - 11 & 𝚌𝚘𝚕𝚘𝚞𝚛 - 2, \\ 𝚘𝚛𝚒𝚐𝚒𝚗 - 3 & 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 10 & 𝚎𝚗𝚍 - 13 & 𝚌𝚘𝚕𝚘𝚞𝚛 - 3, \\ 𝚘𝚛𝚒𝚐𝚒𝚗 - 6 & 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 6 & 𝚎𝚗𝚍 - 12 & 𝚌𝚘𝚕𝚘𝚞𝚛 - 2, \\ 𝚘𝚛𝚒𝚐𝚒𝚗 - 7 & 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 2 & 𝚎𝚗𝚍 - 9 & 𝚌𝚘𝚕𝚘𝚞𝚛 - 3 \end{matrix}〉, 2 \end{matrix})

Figure 5.73.1. The coloured cumulative solution to the Example slot with at most two distinct colours in parallel

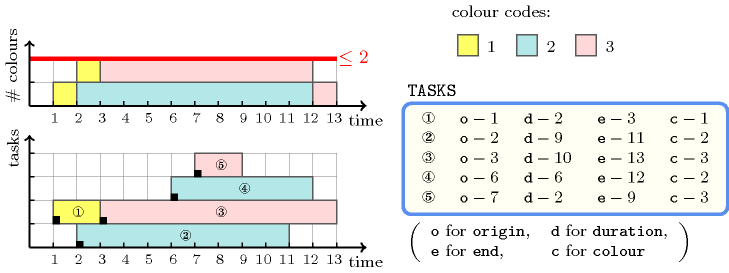
Figure 5.73.1 shows the solution associated with the example. Each rectangle of the figure corresponds to a task of the $𝚌𝚘𝚕𝚘𝚞𝚛𝚎𝚍_𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ constraint. Tasks that have their colour attribute set to 1, 2 and 3 are respectively coloured in yellow, blue and pink. The $𝚌𝚘𝚕𝚘𝚞𝚛𝚎𝚍_𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ constraint holds since at each point in time we do not have more than $𝙻𝙸𝙼𝙸𝚃 = 2$ distinct colours.

Typical

| 𝚃𝙰𝚂𝙺𝚂 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚃𝙰𝚂𝙺𝚂 . 𝚘𝚛𝚒𝚐𝚒𝚗) > 1

𝚛𝚊𝚗𝚐𝚎

(𝚃𝙰𝚂𝙺𝚂 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗) > 1

𝚛𝚊𝚗𝚐𝚎

(𝚃𝙰𝚂𝙺𝚂 . 𝚎𝚗𝚍) > 1

𝚛𝚊𝚗𝚐𝚎

(𝚃𝙰𝚂𝙺𝚂 . 𝚌𝚘𝚕𝚘𝚞𝚛) > 1

𝙻𝙸𝙼𝙸𝚃 <

𝚗𝚟𝚊𝚕

(𝚃𝙰𝚂𝙺𝚂 . 𝚌𝚘𝚕𝚘𝚞𝚛)

Symmetries

Items of $𝚃𝙰𝚂𝙺𝚂$ are permutable.
One and the same constant can be added to the $𝚘𝚛𝚒𝚐𝚒𝚗$ and $𝚎𝚗𝚍$ attributes of all items of $𝚃𝙰𝚂𝙺𝚂$ .
All occurrences of two distinct values of $𝚃𝙰𝚂𝙺𝚂 . 𝚌𝚘𝚕𝚘𝚞𝚛$ can be swapped; all occurrences of a value of $𝚃𝙰𝚂𝙺𝚂 . 𝚌𝚘𝚕𝚘𝚞𝚛$ can be renamed to any unused value.
$𝙻𝙸𝙼𝙸𝚃$ can be increased.

Arg. properties

Contractible wrt. $𝚃𝙰𝚂𝙺𝚂$ .

Usage

Useful for scheduling problems where a machine can only proceed in parallel a maximum number of tasks of distinct type. This condition cannot be modelled by the classical $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ constraint. Also useful for coloured bin packing problems (i.e., $𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 = 1$ ) where each item has a colour and no bin contains items with more than $𝙻𝙸𝙼𝙸𝚃$ distinct colours [DawandeKalagnanamSethuraman98], [GarganiRefalo07], [HeinzSchlechteStephanWinkler12].

Reformulation

The $𝚌𝚘𝚕𝚘𝚞𝚛𝚎𝚍_𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ constraint can be expressed in term of a set of reified constraints and of $| 𝚃𝙰𝚂𝙺𝚂 |$ $𝚗𝚟𝚊𝚕𝚞𝚎$ constraints:

For each pair of tasks $𝚃𝙰𝚂𝙺𝚂 [i], 𝚃𝙰𝚂𝙺𝚂 [j]$ $(i, j \in [1, | 𝚃𝙰𝚂𝙺𝚂 |])$ of the $𝚃𝙰𝚂𝙺𝚂$ collection we create a variable $C_{i j}$ which is set to the colour of task $𝚃𝙰𝚂𝙺𝚂 [j]$ if task $𝚃𝙰𝚂𝙺𝚂 [j]$ overlaps the origin attribute of task $𝚃𝙰𝚂𝙺𝚂 [i]$ , and to the colour of task $𝚃𝙰𝚂𝙺𝚂 [i]$ otherwise:
- If $i = j$ :
  - $C_{i j} = 𝚃𝙰𝚂𝙺𝚂 [i] . 𝚌𝚘𝚕𝚘𝚞𝚛$ .
- If $i \neq j$ :
  - $C_{i j} = 𝚃𝙰𝚂𝙺𝚂 [i] . 𝚌𝚘𝚕𝚘𝚞𝚛 \lor C_{i j} = 𝚃𝙰𝚂𝙺𝚂 [j] . 𝚌𝚘𝚕𝚘𝚞𝚛$ .
  - $((𝚃𝙰𝚂𝙺𝚂 [j] . 𝚘𝚛𝚒𝚐𝚒𝚗 \leq 𝚃𝙰𝚂𝙺𝚂 [i] . 𝚘𝚛𝚒𝚐𝚒𝚗 \land$
    
    $𝚃𝙰𝚂𝙺𝚂 [j] . 𝚎𝚗𝚍 > 𝚃𝙰𝚂𝙺𝚂 [i] . 𝚘𝚛𝚒𝚐𝚒𝚗) \land (C_{i j} = 𝚃𝙰𝚂𝙺𝚂 [j] . 𝚌𝚘𝚕𝚘𝚞𝚛)) \lor$
    
    $((𝚃𝙰𝚂𝙺𝚂 [j] . 𝚘𝚛𝚒𝚐𝚒𝚗 > 𝚃𝙰𝚂𝙺𝚂 [i] . 𝚘𝚛𝚒𝚐𝚒𝚗 \lor$
    
    $𝚃𝙰𝚂𝙺𝚂 [j] . 𝚎𝚗𝚍 \leq 𝚃𝙰𝚂𝙺𝚂 [i] . 𝚘𝚛𝚒𝚐𝚒𝚗) \land (C_{i j} = 𝚃𝙰𝚂𝙺𝚂 [i] . 𝚌𝚘𝚕𝚘𝚞𝚛))$
For each task $𝚃𝙰𝚂𝙺𝚂 [i]$ $(i \in [1, | 𝚃𝙰𝚂𝙺𝚂 |])$ we create a variable $N_{i}$ which gives the number of distinct colours associated with the tasks that overlap the origin of task $𝚃𝙰𝚂𝙺𝚂 [i]$ ( $𝚃𝙰𝚂𝙺𝚂 [i]$ overlaps its own origin) and we impose $N_{i}$ to not exceed the maximum number of distinct colours $𝙻𝙸𝙼𝙸𝚃$ allowed at each instant:
- $N_{i} \geq 1 \land N_{i} \leq 𝙻𝙸𝙼𝙸𝚃$ .
- $𝚗𝚟𝚊𝚕𝚞𝚎$ $(N_{i}, 〈 C_{i 1}, C_{i 2}, \dots, C_{i | 𝚃𝙰𝚂𝙺𝚂 |} 〉)$ .

common keyword: $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ , $𝚝𝚛𝚊𝚌𝚔$ (resource constraint).

related: $𝚗𝚟𝚊𝚕𝚞𝚎$ .

specialisation: $𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝_𝚝𝚊𝚜𝚔𝚜$ (a colour is assigned to each collection of tasks of constraint $𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝_𝚝𝚊𝚜𝚔𝚜$ and a limit of one single colour is enforced).

used in graph description: $𝚗𝚟𝚊𝚕𝚞𝚎𝚜$ .

Keywords

characteristic of a constraint: coloured.

constraint type: scheduling constraint, resource constraint, temporal constraint.

filtering: compulsory part.

modelling: number of distinct values, zero-duration task.

Arc input(s)

$𝚃𝙰𝚂𝙺𝚂$

Arc generator

𝑆𝐸𝐿𝐹

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚝𝚊𝚜𝚔𝚜)

Arc arity

Arc constraint(s)

𝚝𝚊𝚜𝚔𝚜 . 𝚘𝚛𝚒𝚐𝚒𝚗 + 𝚝𝚊𝚜𝚔𝚜 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 = 𝚝𝚊𝚜𝚔𝚜 . 𝚎𝚗𝚍

Graph property(ies)

𝐍𝐀𝐑𝐂

= | 𝚃𝙰𝚂𝙺𝚂 |

Arc input(s)

$𝚃𝙰𝚂𝙺𝚂$ $𝚃𝙰𝚂𝙺𝚂$

Arc generator

𝑃𝑅𝑂𝐷𝑈𝐶𝑇

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚝𝚊𝚜𝚔𝚜 1, 𝚝𝚊𝚜𝚔𝚜 2)

Arc arity

Arc constraint(s)

• 𝚝𝚊𝚜𝚔𝚜 1 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 > 0

• 𝚝𝚊𝚜𝚔𝚜 2 . 𝚘𝚛𝚒𝚐𝚒𝚗 \leq 𝚝𝚊𝚜𝚔𝚜 1 . 𝚘𝚛𝚒𝚐𝚒𝚗

• 𝚝𝚊𝚜𝚔𝚜 1 . 𝚘𝚛𝚒𝚐𝚒𝚗 < 𝚝𝚊𝚜𝚔𝚜 2 . 𝚎𝚗𝚍

Graph class

•

𝙰𝙲𝚈𝙲𝙻𝙸𝙲

•

𝙱𝙸𝙿𝙰𝚁𝚃𝙸𝚃𝙴

•

𝙽𝙾_𝙻𝙾𝙾𝙿

Sets

\begin{matrix} 𝖲𝖴𝖢𝖢 \mapsto \\ [\begin{matrix} 𝚜𝚘𝚞𝚛𝚌𝚎, \\ 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 - 𝚌𝚘𝚕 (\begin{matrix} 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 - 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛), \\ 𝚒𝚝𝚎𝚖 (𝚟𝚊𝚛 - 𝚃𝙰𝚂𝙺𝚂 . 𝚌𝚘𝚕𝚘𝚞𝚛)] \end{matrix}) \end{matrix}] \end{matrix}

Constraint(s) on sets

𝚗𝚟𝚊𝚕𝚞𝚎𝚜

(𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜, \leq, 𝙻𝙸𝙼𝙸𝚃)

Graph model

Same as $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ , except that we use another constraint for computing the resource consumption at each time point.

Parts (A) and (B) of Figure 5.73.2 respectively show the initial and final graph associated with the second graph constraint of the Example slot. On the one hand, each source vertex of the final graph can be interpreted as a time point. On the other hand the successors of a source vertex correspond to those tasks that overlap that time point. The $𝚌𝚘𝚕𝚘𝚞𝚛𝚎𝚍_𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ constraint holds since for each successor set $𝒮$ of the final graph the number of distinct colours of the tasks in $𝒮$ does not exceed the $𝙻𝙸𝙼𝙸𝚃$ 2.

Figure 5.73.2. Initial and final graph of the $𝚌𝚘𝚕𝚘𝚞𝚛𝚎𝚍_𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ constraint

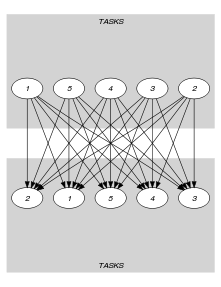
(a)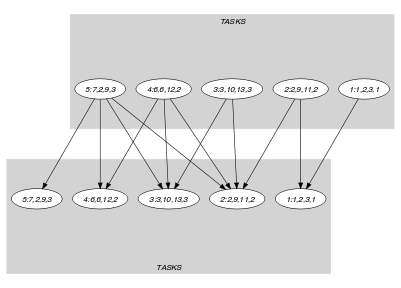

(b)

Signature

Since $𝚃𝙰𝚂𝙺𝚂$ is the maximum number of vertices of the final graph of the first graph constraint we can rewrite $𝐍𝐀𝐑𝐂$ $=$ $| 𝚃𝙰𝚂𝙺𝚂 |$ to $𝐍𝐀𝐑𝐂$ $\geq$ $| 𝚃𝙰𝚂𝙺𝚂 |$ . This leads to simplify $\underset{̲}{\bar{𝐍𝐀𝐑𝐂}}$ to $\bar{𝐍𝐀𝐑𝐂}$ .

Global Constraint Catalog

5. Global Constraint Catalogue

5.73. coloured_cumulative

Figure 5.73.1. The coloured cumulative solution to the Example slot with at most two distinct colours in parallel

Figure 5.73.2. Initial and final graph of the 𝚌𝚘𝚕𝚘𝚞𝚛𝚎𝚍_𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎 constraint

Figure 5.73.2. Initial and final graph of the $𝚌𝚘𝚕𝚘𝚞𝚛𝚎𝚍_𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ constraint