Global Constraint Catalog: Cvec_eq

5.418. vec_eq_tuple

DESCRIPTION

LINKS

GRAPH

Origin

Used for defining $𝚒𝚗_𝚛𝚎𝚕𝚊𝚝𝚒𝚘𝚗$ .

Constraint

$𝚟𝚎𝚌_𝚎𝚚_𝚝𝚞𝚙𝚕𝚎 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚃𝚄𝙿𝙻𝙴)$

Arguments

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚃𝚄𝙿𝙻𝙴$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚕 - 𝚒𝚗𝚝)$

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚃𝚄𝙿𝙻𝙴, 𝚟𝚊𝚕)

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | = | 𝚃𝚄𝙿𝙻𝙴 |

Purpose

Enforce a vector of domain variables to be equal to a tuple of values.

Example

(〈5, 3, 3〉, 〈5, 3, 3〉)

The $𝚟𝚎𝚌_𝚎𝚚_𝚝𝚞𝚙𝚕𝚎$ constraint holds since the first, the second and the third items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 = 〈 5, 3, 3 〉$ are respectively equal to the first, the second and the third items of $𝚃𝚄𝙿𝙻𝙴 = 〈 5, 3, 3 〉$ .

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 1

𝚛𝚊𝚗𝚐𝚎

(𝚃𝚄𝙿𝙻𝙴 . 𝚟𝚊𝚕) > 1

Symmetries

Arguments are permutable w.r.t. permutation $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚃𝚄𝙿𝙻𝙴)$ .
Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ and $𝚃𝚄𝙿𝙻𝙴$ are permutable (same permutation used).

Arg. properties

Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ and $𝚃𝚄𝙿𝙻𝙴$ (remove items from same position).

Used in

$𝚒𝚗_𝚛𝚎𝚕𝚊𝚝𝚒𝚘𝚗$ .

See also

generalisation: $𝚕𝚎𝚡_𝚎𝚚𝚞𝚊𝚕$ ( $𝚒𝚗𝚝𝚎𝚐𝚎𝚛$ replaced by $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ in second argument).

implies: $𝚕𝚎𝚡_𝚎𝚚𝚞𝚊𝚕$ .

Keywords

characteristic of a constraint: tuple.

constraint type: value constraint.

filtering: arc-consistency.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ $𝚃𝚄𝙿𝙻𝙴$

Arc generator

𝑃𝑅𝑂𝐷𝑈𝐶𝑇

(=) \mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜, 𝚝𝚞𝚙𝚕𝚎)

Arc arity

Arc constraint(s)

𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 . 𝚟𝚊𝚛 = 𝚝𝚞𝚙𝚕𝚎 . 𝚟𝚊𝚕

Graph property(ies)

𝐍𝐀𝐑𝐂

= | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

Graph model

Parts (A) and (B) of Figure 5.418.1 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐀𝐑𝐂$ graph property, the arcs of the final graph are stressed in bold.

Figure 5.418.1. Initial and final graph of the $𝚟𝚎𝚌_𝚎𝚚_𝚝𝚞𝚙𝚕𝚎$ constraint


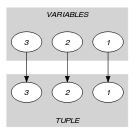
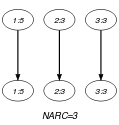
(a)	(b)

Signature

Since we use the arc generator $𝑃𝑅𝑂𝐷𝑈𝐶𝑇 (=)$ on the collections $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ and $𝚃𝚄𝙿𝙻𝙴$ , and because of the restriction $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | = | 𝚃𝚄𝙿𝙻𝙴 |$ , the maximum number of arcs of the final graph is equal to $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |$ . Therefore we can rewrite the graph property $𝐍𝐀𝐑𝐂 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |$ to $𝐍𝐀𝐑𝐂 \geq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |$ and simplify $\underset{̲}{\bar{𝐍𝐀𝐑𝐂}}$ to $\bar{𝐍𝐀𝐑𝐂}$ .

Global Constraint Catalog

5. Global Constraint Catalogue

5.418. vec_eq_tuple

Figure 5.418.1. Initial and final graph of the 𝚟𝚎𝚌_𝚎𝚚_𝚝𝚞𝚙𝚕𝚎 constraint

Figure 5.418.1. Initial and final graph of the $𝚟𝚎𝚌_𝚎𝚚_𝚝𝚞𝚙𝚕𝚎$ constraint