5.230. lex_greatereq
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
CHIP
- Constraint
- Synonyms
, , , , , .
- Arguments
- Restrictions
- Purpose
is lexicographically greater than or equal to . Given two vectors, and of components, and , is lexicographically greater than or equal to if and only if or or and is lexicographically greater than or equal to .
- Example
-
The constraints associated with the first and second examples hold since:
Within the first example is lexicographically greater than or equal to .
Within the second example is lexicographically greater than or equal to .
- Typical
- Symmetries
- Arg. properties
Suffix-contractible wrt. and (remove items from same position).
- Remark
A multiset ordering constraint and its corresponding filtering algorithm are described in [FriHniKizMigWal03].
- Algorithm
The first filtering algorithm maintaining arc-consistency for this constraint was presented in [FrischHnichKiziltanMiguelWalsh02]. A second filtering algorithm maintaining arc-consistency and detecting entailment in a more eager way, was given in [BeldiceanuCarlsson02b]. This second algorithm was derived from a deterministic finite automata. A third filtering algorithm extending the algorithm presented in [FrischHnichKiziltanMiguelWalsh02] detecting entailment is given in the PhD thesis of Z. Kızıltan [Kiziltan04]. The previous thesis [Kiziltan04] presents also a filtering algorithm handling the fact that a given variable has more than one occurrence. Finally, T. Frühwirth shows how to encode lexicographic ordering constraints within the context of CHR [Fruhwirth98] in [Fruhwirth06].
- Reformulation
The following reformulations in term of arithmetic and/or logical expressions exist for enforcing the lexicographically greater than or equal to constraint. The first one converts and into numbers and post an inequality constraint. It assumes all components of and to be within :
Since the previous reformulation can only be used with small values of and , W. Harvey came up with the following alternative model that maintains arc-consistency:
Finally, the lexicographically greater than or equal to constraint can be expressed as a conjunction or a disjunction of constraints:
When used separately, the two previous logical decompositions do not maintain arc-consistency.
- Systems
lexEq in Choco, rel in Gecode, lex_greatereq in MiniZinc, lex_chain in SICStus.
- See also
common keyword: , , , , (lexicographic order), (vector).
implied by: , , .
- Keywords
characteristic of a constraint: vector, automaton, automaton without counters, reified automaton constraint, derived collection.
constraint network structure: Berge-acyclic constraint network.
constraint type: order constraint.
filtering: duplicated variables, arc-consistency.
heuristics: heuristics and lexicographical ordering.
symmetry: symmetry, matrix symmetry, lexicographic order, multiset ordering.
- Derived Collections
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
Parts (A) and (B) of Figure 5.230.1 respectively show the initial and final graph associated with the first example of the Example slot. Since we use the graph property we show on the final graph the following information:
The vertices, which respectively correspond to the start and the end of the required path, are stressed in bold.
The arcs on the required path are also stressed in bold.
Figure 5.230.1. Initial and final graph of the constraint
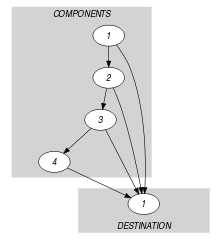
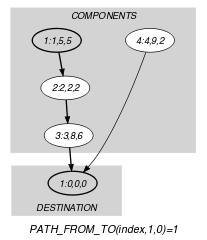
(a) (b) The vertices of the initial graph are generated in the following way:
We create a vertex for each pair of components that both have the same index .
We create an additional dummy vertex called .
The arcs of the initial graph are generated in the following way:
We create an arc between and . When was generated from the last components of both vectors We associate to this arc the arc constraint ; Otherwise we associate to this arc the arc constraint ;
We create an arc between and . We associate to this arc the arc constraint .
The constraint holds when there exist a path from to . This path can be interpreted as a maximum sequence of equality constraints on the prefix of both vectors, possibly followed by a greater than constraint.
- Signature
Since the maximum value returned by the graph property is equal to 1 we can rewrite to . Therefore we simplify to .
- Automaton
Figure 5.230.2 depicts the automaton associated with the constraint. Let and respectively be the attributes of the items of the and the collections. To each pair corresponds a signature variable as well as the following signature constraint: .
Figure 5.230.2. Automaton of the constraint
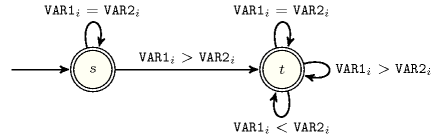
Figure 5.230.3. Hypergraph of the reformulation corresponding to the automaton of the constraint