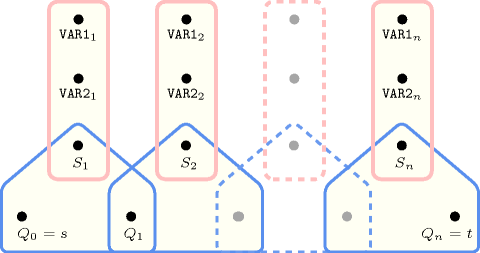
5.227. lex_different
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
- Constraint
- Synonyms
, .
- Arguments
- Restrictions
- Purpose
Vectors and differ in at least one component.
- Example
-
The constraint holds since and differ in their second component.
- Typical
- Symmetries
Arguments are permutable w.r.t. permutation .
Items of and are permutable (same permutation used).
- Arg. properties
Extensible wrt. and (add items at same position).
- Reformulation
The constraint can be expressed in term of the following disjunction of disequality constraints .
- Used in
- See also
common keyword: , (vector).
implied by: , , , .
- Keywords
characteristic of a constraint: vector, disequality, automaton, automaton without counters, reified automaton constraint.
constraint network structure: Berge-acyclic constraint network.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
Parts (A) and (B) of Figure 5.227.1 respectively show the initial and final graph associated with the Example slot. Since we use the graph property, the unique arc of the final graph is stressed in bold. It corresponds to a component where the two vectors differ.
Figure 5.227.1. Initial and final graph of the constraint
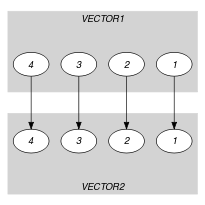
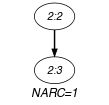
(a) (b)
- Automaton
Figure 5.227.2 depicts the automaton associated with the constraint. Let and respectively be the attributes of the items of the and the collections. To each pair corresponds a 0-1 signature variable as well as the following signature constraint: .
Figure 5.227.2. Automaton of the constraint
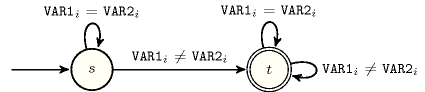
Figure 5.227.3. Hypergraph of the reformulation corresponding to the automaton of the constraint