Global Constraint Catalog: Cuses

5.416. uses

DESCRIPTION

LINKS

GRAPH

Origin

[BessiereHebrardHnichKiziltanWalsh05IJCAI]

Constraint

$𝚞𝚜𝚎𝚜 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2)$

Arguments

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝚖𝚒𝚗 (1, | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 |) \geq 𝚖𝚒𝚗 (1, | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚟𝚊𝚛)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2, 𝚟𝚊𝚛)

Purpose

The set of values assigned to the variables of the collection of variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ is included within the set of values assigned to the variables of the collection of variables $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ .

Example

(〈3, 3, 4, 6〉, 〈3, 4, 4, 4, 4〉)

The $𝚞𝚜𝚎𝚜$ constraint holds since the set of values ${3, 4}$ assigned to the items of collection $〈 3, 4, 4, 4, 4 〉$ is included within the set of values ${3, 4, 6}$ occurring within $〈 3, 3, 4, 6 〉$ .

All solutions

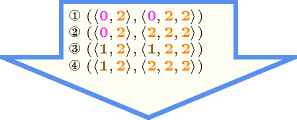
Figure 5.416.1 gives all solutions to the following non ground instance of the $𝚞𝚜𝚎𝚜$ constraint: $U_{1} \in [0, 1]$ , $U_{2} \in [1, 2]$ , $V_{1} \in [0, 2]$ , $V_{2} \in [2, 4]$ , $V_{3} \in [2, 4]$ , $𝚞𝚜𝚎𝚜$ $(〈 U_{1}, U_{2} 〉, 〈 V_{1}, V_{2}, V_{3} 〉)$ .

Figure 5.416.1. All solutions corresponding to the non ground example of the $𝚞𝚜𝚎𝚜$ constraint of the All solutions slot where identical values are coloured in the same way in both collections

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛) > 1

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛) > 1

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ are permutable.
Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ are permutable.
All occurrences of two distinct values in $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛$ or $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛$ can be swapped; all occurrences of a value in $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛$ or $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛$ can be renamed to any unused value.

Arg. properties

Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ .
Extensible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ .
Aggregate: $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 (𝚞𝚗𝚒𝚘𝚗)$ , $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 (𝚞𝚗𝚒𝚘𝚗)$ .

Remark

It was shown in [BessiereHebrardHnichKiziltanWalsh05IJCAI] that, finding out whether a $𝚞𝚜𝚎𝚜$ constraint has a solution or not is NP-hard. This was achieved by reduction from 3-SAT.

See also

generalisation: $𝚌𝚘𝚖𝚖𝚘𝚗$ .

implied by: $𝚞𝚜𝚎𝚍_𝚋𝚢$ .

related: $𝚛𝚘𝚘𝚝𝚜$ .

Keywords

complexity: 3-SAT.

constraint arguments: constraint between two collections of variables.

final graph structure: acyclic, bipartite, no loop.

modelling: inclusion.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$

Arc generator

𝑃𝑅𝑂𝐷𝑈𝐶𝑇

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 = 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛

Graph property(ies)

𝐍𝐒𝐈𝐍𝐊

= | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |

Graph class

•

𝙰𝙲𝚈𝙲𝙻𝙸𝙲

•

𝙱𝙸𝙿𝙰𝚁𝚃𝙸𝚃𝙴

•

𝙽𝙾_𝙻𝙾𝙾𝙿

Graph model

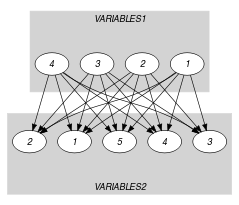
Parts (A) and (B) of Figure 5.416.2 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐒𝐈𝐍𝐊$ graph property, the sink vertices of the final graph are stressed with a double circle. Note that all the vertices corresponding to the variables that take values 9 or 2 were removed from the final graph since there is no arc for which the associated equality constraint holds.

Figure 5.416.2. Initial and final graph of the $𝚞𝚜𝚎𝚜$ constraint

(a)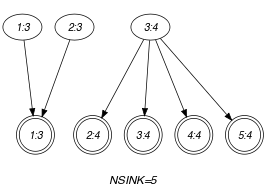

(b)

cleardoublepageeven

Global Constraint Catalog

5. Global Constraint Catalogue

5.416. uses

Figure 5.416.1. All solutions corresponding to the non ground example of the 𝚞𝚜𝚎𝚜 constraint of the All solutions slot where identical values are coloured in the same way in both collections

Figure 5.416.2. Initial and final graph of the 𝚞𝚜𝚎𝚜 constraint

Figure 5.416.1. All solutions corresponding to the non ground example of the $𝚞𝚜𝚎𝚜$ constraint of the All solutions slot where identical values are coloured in the same way in both collections

Figure 5.416.2. Initial and final graph of the $𝚞𝚜𝚎𝚜$ constraint