Global Constraint Catalog: Cint_value_precede

5.196. int_value_precede_chain

DESCRIPTION

LINKS

AUTOMATON

Origin

[YatChiuLawJimmyLee04]

Constraint

$𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎_𝚌𝚑𝚊𝚒𝚗 (𝚅𝙰𝙻𝚄𝙴𝚂, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Synonyms

$𝚙𝚛𝚎𝚌𝚎𝚍𝚎$ , $𝚙𝚛𝚎𝚌𝚎𝚍𝚎𝚗𝚌𝚎$ , $𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎_𝚌𝚑𝚊𝚒𝚗$ .

Arguments

$𝚅𝙰𝙻𝚄𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚒𝚗𝚝)$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝙻𝚄𝙴𝚂, 𝚟𝚊𝚛)

𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝

(𝚅𝙰𝙻𝚄𝙴𝚂, 𝚟𝚊𝚛)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

Purpose

Assuming $n$ denotes the number of items of the $𝚅𝙰𝙻𝚄𝙴𝚂$ collection, the following condition holds for every $i \in [1, n - 1]$ : When it is defined, the first occurrence of the ${(i + 1)}^{t h}$ value of the $𝚅𝙰𝙻𝚄𝙴𝚂$ collection should be preceded by the first occurrence of the $i^{t h}$ value of the $𝚅𝙰𝙻𝚄𝙴𝚂$ collection.

Example

(〈4, 0, 1〉, 〈4, 0, 6, 1, 0〉)

The $𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎_𝚌𝚑𝚊𝚒𝚗$ constraint holds since within the sequence 4, 0, 6, 1, 0:

The first occurrence of value 4 occurs before the first occurrence of value 0.
The first occurrence of value 0 occurs before the first occurrence of value 1.

Typical

| 𝚅𝙰𝙻𝚄𝙴𝚂 | > 1

𝚜𝚝𝚛𝚒𝚌𝚝𝚕𝚢_𝚒𝚗𝚌𝚛𝚎𝚊𝚜𝚒𝚗𝚐

(𝚅𝙰𝙻𝚄𝙴𝚂)

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > | 𝚅𝙰𝙻𝚄𝙴𝚂 |

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 1

𝚞𝚜𝚎𝚍_𝚋𝚢

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚅𝙰𝙻𝚄𝙴𝚂)

Symmetry

An occurrence of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ that does not occur in $𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚛$ can be replaced by any other value that also does not occur in $𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚛$ .

Arg. properties

Contractible wrt. $𝚅𝙰𝙻𝚄𝙴𝚂$ .
Suffix-contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .
Aggregate: $𝚅𝙰𝙻𝚄𝙴𝚂 (𝚒𝚍)$ , $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 (𝚞𝚗𝚒𝚘𝚗)$ .

Usage

The $𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎_𝚌𝚑𝚊𝚒𝚗$ constraint is useful for breaking symmetries in graph colouring problems. We set a $𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎_𝚌𝚑𝚊𝚒𝚗$ constraint on all variables $V_{1}, V_{2}, \dots, V_{n}$ associated with the vertices of the graph to colour, where we state that the first occurrence of colour $i$ should be located before the first occurrence of colour $i + 1$ within the sequence $V_{1}, V_{2}, \dots, V_{n}$ .

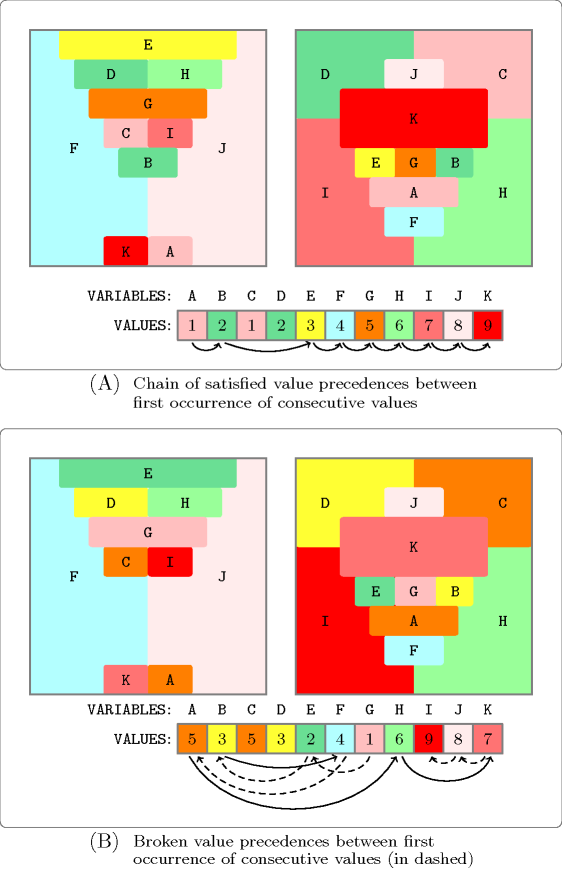
Figure 5.196.1 illustrates the problem of colouring earth and mars from Thom Sulanke. Part (A) of Figure 5.196.1 provides a solution where the first occurrence of each value of $i$ , $(i \in {1, 2, \dots, 8})$ is located before the first occurrence of value $i + 1$ . This is obtained by using the following constraints:

\{\begin{matrix} 𝙰 \neq 𝙱, 𝙰 \neq 𝙴, 𝙰 \neq 𝙵, 𝙰 \neq 𝙶, 𝙰 \neq 𝙷, 𝙰 \neq 𝙸, 𝙰 \neq 𝙹, 𝙰 \neq 𝙺, \\ 𝙱 \neq 𝙰, 𝙱 \neq 𝙲, 𝙱 \neq 𝙵, 𝙱 \neq 𝙶, 𝙱 \neq 𝙷, 𝙱 \neq 𝙸, 𝙱 \neq 𝙹, 𝙱 \neq 𝙺, \\ 𝙲 \neq 𝙱, 𝙲 \neq 𝙳, 𝙲 \neq 𝙵, 𝙲 \neq 𝙶, 𝙲 \neq 𝙷, 𝙲 \neq 𝙸, 𝙲 \neq 𝙹, 𝙲 \neq 𝙺, \\ 𝙳 \neq 𝙲, 𝙳 \neq 𝙴, 𝙳 \neq 𝙵, 𝙳 \neq 𝙶, 𝙳 \neq 𝙷, 𝙳 \neq 𝙸, 𝙳 \neq 𝙹, 𝙳 \neq 𝙺, \\ 𝙴 \neq 𝙰, 𝙴 \neq 𝙳, 𝙴 \neq 𝙵, 𝙴 \neq 𝙶, 𝙴 \neq 𝙷, 𝙴 \neq 𝙸, 𝙴 \neq 𝙹, 𝙴 \neq 𝙺, \\ 𝙵 \neq 𝙰, 𝙵 \neq 𝙱, 𝙵 \neq 𝙲, 𝙵 \neq 𝙳, 𝙵 \neq 𝙴, 𝙵 \neq 𝙶, 𝙵 \neq 𝙷, 𝙵 \neq 𝙸, 𝙵 \neq 𝙹, 𝙵 \neq 𝙺, \\ 𝙶 \neq 𝙰, 𝙶 \neq 𝙱, 𝙶 \neq 𝙲, 𝙶 \neq 𝙳, 𝙶 \neq 𝙴, 𝙶 \neq 𝙵, 𝙶 \neq 𝙷, 𝙶 \neq 𝙸, 𝙶 \neq 𝙹, 𝙶 \neq 𝙺, \\ 𝙷 \neq 𝙰, 𝙷 \neq 𝙱, 𝙷 \neq 𝙲, 𝙷 \neq 𝙳, 𝙷 \neq 𝙴, 𝙷 \neq 𝙵, 𝙷 \neq 𝙶, 𝙷 \neq 𝙸, 𝙷 \neq 𝙹, 𝙷 \neq 𝙺, \\ 𝙸 \neq 𝙰, 𝙸 \neq 𝙱, 𝙸 \neq 𝙲, 𝙸 \neq 𝙳, 𝙸 \neq 𝙴, 𝙸 \neq 𝙵, 𝙸 \neq 𝙶, 𝙸 \neq 𝙷, 𝙸 \neq 𝙹, 𝙸 \neq 𝙺, \\ 𝙹 \neq 𝙰, 𝙹 \neq 𝙱, 𝙹 \neq 𝙲, 𝙹 \neq 𝙳, 𝙹 \neq 𝙴, 𝙹 \neq 𝙵, 𝙹 \neq 𝙶, 𝙹 \neq 𝙷, 𝙹 \neq 𝙸, 𝙹 \neq 𝙺, \\ 𝙺 \neq 𝙰, 𝙺 \neq 𝙱, 𝙺 \neq 𝙲, 𝙺 \neq 𝙳, 𝙺 \neq 𝙴, 𝙺 \neq 𝙵, 𝙺 \neq 𝙶, 𝙺 \neq 𝙷, 𝙺 \neq 𝙸, 𝙺 \neq 𝙹, \\ 𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎_𝚌𝚑𝚊𝚒𝚗 (〈1, 2, 3, 4, 5, 6, 7, 8, 9〉, 〈𝙰, 𝙱, 𝙲, 𝙳, 𝙴, 𝙵, 𝙶, 𝙷, 𝙸, 𝙹, 𝙺〉) . \end{matrix}

Part (B) provides a symmetric solution where the value precedence constraints between the pairs of values $(1, 2)$ , $(2, 3)$ , $(4, 5)$ , $(7, 8)$ and $(8, 9)$ are all violated (each violation is depicted by a dashed arc).

Figure 5.196.1. Using the $𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎_𝚌𝚑𝚊𝚒𝚗$ constraint for breaking symmetries in graph colouring problems; there is an arc between the first occurrence of value $v$ $(1 \leq v \leq 8)$ in the sequence of variables $𝙰$ , $𝙱$ , $𝙲$ , $𝙳$ , $𝙴$ , $𝙵$ , $𝙶$ , $𝙷$ , $𝙸$ , $𝙹$ , $𝙺$ , and the first occurrence of value $v + 1$ (a plain arc if the corresponding value precedence constraint holds, a dashed arc otherwise)

Remark

When we have more than one class of interchangeable values (i.e., a partition of interchangeable values) we can use one $𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎_𝚌𝚑𝚊𝚒𝚗$ constraint for breaking value symmetry in each class of interchangeable values. However it was shown in [Walsh07] that enforcing arc-consistency for such a conjunction of $𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎_𝚌𝚑𝚊𝚒𝚗$ constraints is NP-hard.

Algorithm

The 2004 reformulation [Beldiceanu04] associated with the automaton of the Automaton slot achieves arc-consistency since the corresponding constraint network is a Berge-acyclic constraint network. Later on, another formulation into a sequence of ternary sliding constraints was proposed by [Walsh06]. It also achieves arc-consistency for the same reason.

Systems

precede in Gecode, value_precede_chain in MiniZinc.

See also

specialisation: $𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎$ ( $𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ of at least 2 $𝚟𝚊𝚕𝚞𝚎𝚜$ replaced by $𝚜𝚎𝚚𝚞𝚎𝚗𝚌𝚎$ of 2 $𝚟𝚊𝚕𝚞𝚎𝚜$ ).

Keywords

characteristic of a constraint: automaton, automaton without counters, reified automaton constraint.

constraint network structure: Berge-acyclic constraint network.

constraint type: order constraint.

filtering: arc-consistency.

problems: graph colouring.

symmetry: symmetry, indistinguishable values, value precedence.

Automaton

Figure 5.196.2 depicts the automaton associated with the $𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎_𝚌𝚑𝚊𝚒𝚗$ constraint. Let $n$ and $m$ respectively denote the number of variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection and the number of values of the $𝚅𝙰𝙻𝚄𝙴𝚂$ collection. Let ${𝚅𝙰𝚁}_{i}$ be the $i^{t h}$ variable of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection. Let ${𝚟𝚊𝚕}_{v}$ $(1 \leq v \leq m)$ denote the $v^{t h}$ value of the $𝚅𝙰𝙻𝚄𝙴𝚂$ collection.

Figure 5.196.2. Automaton of the $𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎_𝚌𝚑𝚊𝚒𝚗$ constraint (state $s_{i}$ means that (1) each value ${𝚟𝚊𝚕}_{1}, {𝚟𝚊𝚕}_{2}, \dots, {𝚟𝚊𝚕}_{i}$ was already encountered at least once, and that (2) value ${𝚟𝚊𝚕}_{i + 1}$ was not yet found)

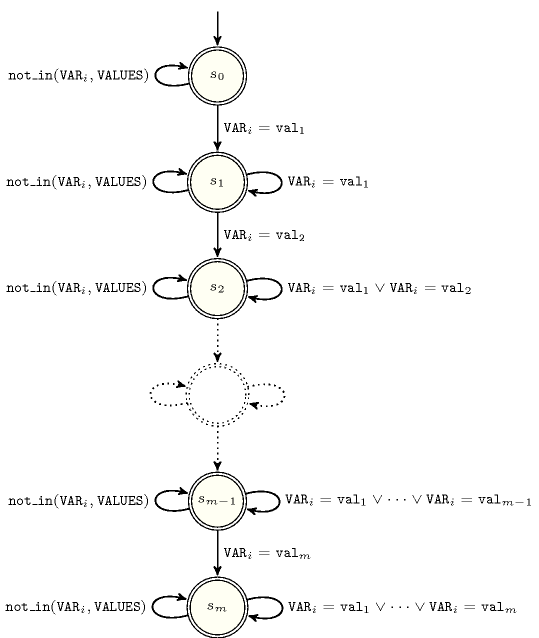
Figure 5.196.3. Hypergraph of the reformulation corresponding to the automaton of the $𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎_𝚌𝚑𝚊𝚒𝚗$ constraint (since all states of the automaton are accepting there is no restriction on the last variable $Q_{n}$ )

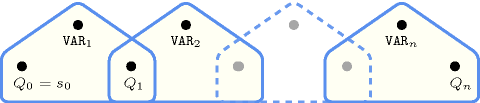
We now show how to construct such an automaton systematically. For this purpose let us first introduce some notations:

Without loss of generality we assume that we have at least two values (i.e., $m \geq 2$ ).
Let $𝒞$ be the set of values that can be potentially assigned to a variable of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection, but which do not belong to the values of the $𝚅𝙰𝙻𝚄𝙴𝚂$ collection (i.e., $𝒞 = (𝑑𝑜𝑚 ({𝚅𝙰𝚁}_{1}) \cup 𝑑𝑜𝑚 ({𝚅𝙰𝚁}_{2}) \cup \dots \cup 𝑑𝑜𝑚 ({𝚅𝙰𝚁}_{n}) - {{𝚟𝚊𝚕}_{1}, {𝚟𝚊𝚕}_{2}, \dots, {𝚟𝚊𝚕}_{m}} = {w_{1}, w_{2}, \dots, w_{| 𝒞 |}}$ .

The states and transitions of the automaton are respectively defined in the following way:

We have $m + 1$ states labelled $s_{0}, s_{1}, \dots, s_{m}$ from which $s_{0}$ is the initial state. All states are accepting states.
We have the following three sets of transitions:
1. For all $v \in [0, m - 1]$ , a transition from $s_{v}$ to $s_{v + 1}$ labelled by value ${𝚟𝚊𝚕}_{v + 1}$ . Each transition of this type will be triggered on the first occurrence of value ${𝚟𝚊𝚕}_{v + 1}$ within the variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection.
2. For all $v \in [1, m]$ and for all $w \in [1, v]$ , a self loop on $s_{v}$ labelled by value ${𝚟𝚊𝚕}_{w}$ . Such transitions encode the fact that we stay in the same state as long as we have a value that was already encountered.
3. If the set $𝒞$ is not empty, then for all $v \in [0, m]$ a self loop on $s_{v}$ labelled by the fact that we take a value not in $𝚅𝙰𝙻𝚄𝙴𝚂$ (i.e., a value in $𝒞$ ). This models the fact that, encountering a value that does not belong to the set of values of the $𝚅𝙰𝙻𝚄𝙴𝚂$ collection, leaves us in the same state.

Global Constraint Catalog

5. Global Constraint Catalogue

5.196. int_value_precede_chain

Figure 5.196.3. Hypergraph of the reformulation corresponding to the automaton of the 𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎_𝚌𝚑𝚊𝚒𝚗 constraint (since all states of the automaton are accepting there is no restriction on the last variable Q n )

Figure 5.196.3. Hypergraph of the reformulation corresponding to the automaton of the $𝚒𝚗𝚝_𝚟𝚊𝚕𝚞𝚎_𝚙𝚛𝚎𝚌𝚎𝚍𝚎_𝚌𝚑𝚊𝚒𝚗$ constraint (since all states of the automaton are accepting there is no restriction on the last variable $Q_{n}$ )