5. Global Constraint Catalogue

5.88. consecutive_values

DESCRIPTION

LINKS

Origin

Derived from $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜$ .

Constraint

$𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Argument

𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂

𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)

Restriction

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

Purpose

Constraint the difference between the largest and the smallest values of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection to be equal to the number of distinct values assigned to the variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ collection minus one (i.e., there is no holes at all within the used values).

Example

(〈5, 4, 3, 5〉)

The $𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜$ constraint holds since all values between value 3 and value 5 are actually used.

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛) > 1

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are permutable.
One and the same constant can be added to the $𝚟𝚊𝚛$ attribute of all items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

Counting

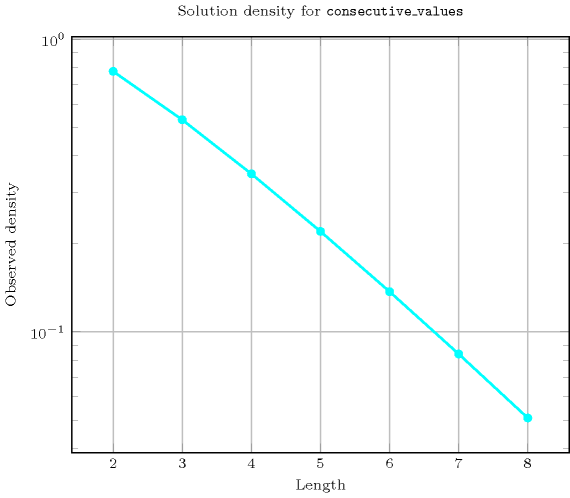
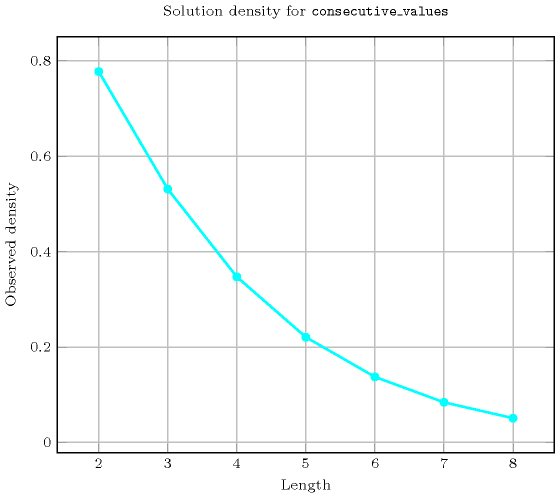
Length ( $n$ )	2	3	4	5	6	7	8
Solutions	7	34	217	1716	16159	176366	2187637

Number of solutions for $𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜$ : domains $0 . . n$

ctrs/consecutive_values-1-tikz

ctrs/consecutive_values-2-tikz

See also

implied by: $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕$ , $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜$ , $𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚘𝚗𝚝𝚒𝚐𝚞𝚒𝚝𝚢$ .

used in reformulation: $𝚗𝚟𝚊𝚕𝚞𝚎$ .

Keywords

characteristic of a constraint: sort based reformulation.

constraint type: value constraint, predefined constraint.

Cond. implications

$𝚌𝚘𝚗𝚜𝚎𝚌𝚞𝚝𝚒𝚟𝚎_𝚟𝚊𝚕𝚞𝚎𝚜 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

with $| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | >$ $𝚛𝚊𝚗𝚐𝚎$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛)$

implies $𝚜𝚘𝚖𝚎_𝚎𝚚𝚞𝚊𝚕$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$ .