Global Constraint Catalog: Ccommon

5.78. common_partition

DESCRIPTION

LINKS

GRAPH

Origin

Derived from $𝚌𝚘𝚖𝚖𝚘𝚗$ .

Constraint

$𝚌𝚘𝚖𝚖𝚘𝚗_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗 (\begin{matrix} 𝙽𝙲𝙾𝙼𝙼𝙾𝙽 1, \\ 𝙽𝙲𝙾𝙼𝙼𝙾𝙽 2, \\ 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, \\ 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2, \\ 𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂 \end{matrix})$

Type

𝚅𝙰𝙻𝚄𝙴𝚂

𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚕 - 𝚒𝚗𝚝)

Arguments

$𝙽𝙲𝙾𝙼𝙼𝙾𝙽 1$	$𝚍𝚟𝚊𝚛$
$𝙽𝙲𝙾𝙼𝙼𝙾𝙽 2$	$𝚍𝚟𝚊𝚛$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚙 - 𝚅𝙰𝙻𝚄𝙴𝚂)$

Restrictions

| 𝚅𝙰𝙻𝚄𝙴𝚂 | \geq 1

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝙻𝚄𝙴𝚂, 𝚟𝚊𝚕)

𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝

(𝚅𝙰𝙻𝚄𝙴𝚂, 𝚟𝚊𝚕)

𝙽𝙲𝙾𝙼𝙼𝙾𝙽 1 \geq 0

𝙽𝙲𝙾𝙼𝙼𝙾𝙽 1 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 |

𝙽𝙲𝙾𝙼𝙼𝙾𝙽 2 \geq 0

𝙽𝙲𝙾𝙼𝙼𝙾𝙽 2 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚟𝚊𝚛)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2, 𝚟𝚊𝚛)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂, 𝚙)

| 𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂 | \geq 2

Purpose

$𝙽𝙲𝙾𝙼𝙼𝙾𝙽 1$ is the number of variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ collection taking a value in a partition derived from the values assigned to the variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ and from $𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂$ .

$𝙽𝙲𝙾𝙼𝙼𝙾𝙽 2$ is the number of variables of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ collection taking a value in a partition derived from the values assigned to the variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ and from $𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂$ .

Example

(\begin{matrix} 3, 4, 〈2, 3, 6, 0〉, \\ 〈0, 6, 3, 3, 7, 1〉, \\ 〈𝚙 - 〈1, 3〉, 𝚙 - 〈4〉, 𝚙 - 〈2, 6〉〉 \end{matrix})

In the example, the last argument $𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂$ defines the partitions $𝚙 - 〈 1, 3 〉$ , $𝚙 - 〈 4 〉$ and $𝚙 - 〈 2, 6 〉$ . As a consequence the first three items of collection $〈 2, 3, 6, 0 〉$ respectively correspond to the partitions $𝚙 - 〈 2, 6 〉$ , $𝚙 - 〈 1, 3 〉$ , and $𝚙 - 〈 2, 6 〉$ . Similarly the items of collection $〈 0, 6, 3, 3, 7, 1 〉$ (from which we remove items 0 and 7 since they do not belong to any partition) respectively correspond to the partitions $𝚙 - 〈 2, 6 〉$ , $𝚙 - 〈 1, 3 〉$ , $𝚙 - 〈 1, 3 〉$ , and $𝚙 - 〈 1, 3 〉$ . The $𝚌𝚘𝚖𝚖𝚘𝚗_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗$ constraint holds since:

Its first argument $𝙽𝙲𝙾𝙼𝙼𝙾𝙽 1 = 3$ is the number of partitions associated with the items of collection $〈 2, 3, 6, 0 〉$ that also correspond to partitions associated with $〈 0, 6, 3, 3, 7, 1 〉$ .
Its second argument $𝙽𝙲𝙾𝙼𝙼𝙾𝙽 2 = 4$ is the number of partitions associated with the items of collection $〈 0, 6, 3, 3, 7, 1 〉$ that also correspond to partitions associated with $〈 2, 3, 6, 0 〉$ .

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛) > 1

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛) > 1

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | > | 𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂 |

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 | > | 𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂 |

Symmetries

Arguments are permutable w.r.t. permutation $(𝙽𝙲𝙾𝙼𝙼𝙾𝙽 1, 𝙽𝙲𝙾𝙼𝙼𝙾𝙽 2)$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2)$ $(𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂)$ .
Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ are permutable.
Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ are permutable.
Items of $𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂$ are permutable.
Items of $𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂 . 𝚙$ are permutable.
An occurrence of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛$ can be replaced by any other value that also belongs to the same partition of $𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂$ .
An occurrence of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛$ can be replaced by any other value that also belongs to the same partition of $𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂$ .

Arg. properties

Functional dependency: $𝙽𝙲𝙾𝙼𝙼𝙾𝙽 1$ determined by $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ , $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ and $𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂$ .
Functional dependency: $𝙽𝙲𝙾𝙼𝙼𝙾𝙽 2$ determined by $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ , $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ and $𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂$ .

See also

specialisation: $𝚌𝚘𝚖𝚖𝚘𝚗$ ( $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎 \in 𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗$ replaced by $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ ).

used in graph description: $𝚒𝚗_𝚜𝚊𝚖𝚎_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗$ .

Keywords

characteristic of a constraint: partition.

constraint arguments: constraint between two collections of variables, pure functional dependency.

final graph structure: acyclic, bipartite, no loop.

modelling: functional dependency.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$

Arc generator

𝑃𝑅𝑂𝐷𝑈𝐶𝑇

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

𝚒𝚗_𝚜𝚊𝚖𝚎_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗

(𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛, 𝙿𝙰𝚁𝚃𝙸𝚃𝙸𝙾𝙽𝚂)

Graph property(ies)

•

𝐍𝐒𝐎𝐔𝐑𝐂𝐄

= 𝙽𝙲𝙾𝙼𝙼𝙾𝙽 1

•

𝐍𝐒𝐈𝐍𝐊

= 𝙽𝙲𝙾𝙼𝙼𝙾𝙽 2

Graph class

•

𝙰𝙲𝚈𝙲𝙻𝙸𝙲

•

𝙱𝙸𝙿𝙰𝚁𝚃𝙸𝚃𝙴

•

𝙽𝙾_𝙻𝙾𝙾𝙿

Graph model

Parts (A) and (B) of Figure 5.78.1 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐒𝐎𝐔𝐑𝐂𝐄$ and $𝐍𝐒𝐈𝐍𝐊$ graph properties, the source and sink vertices of the final graph are stressed with a double circle. Since the graph has only 3 sources and 4 sinks the variables $𝙽𝙲𝙾𝙼𝙼𝙾𝙽 1$ and $𝙽𝙲𝙾𝙼𝙼𝙾𝙽 2$ are respectively equal to 3 and 4. Note that the vertices corresponding to the variables that take values 0 or 7 were removed from the final graph since there is no arc for which the associated $𝚒𝚗_𝚜𝚊𝚖𝚎_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗$ constraint holds.

Figure 5.78.1. Initial and final graph of the $𝚌𝚘𝚖𝚖𝚘𝚗_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗$ constraint


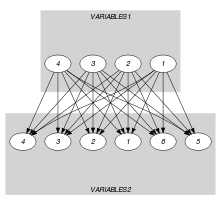
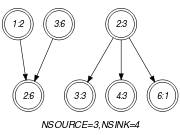
(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.78. common_partition

Figure 5.78.1. Initial and final graph of the 𝚌𝚘𝚖𝚖𝚘𝚗_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗 constraint

Figure 5.78.1. Initial and final graph of the $𝚌𝚘𝚖𝚖𝚘𝚗_𝚙𝚊𝚛𝚝𝚒𝚝𝚒𝚘𝚗$ constraint