Global Constraint Catalog: Cdisj

5.122. disj

DESCRIPTION

LINKS

GRAPH

Origin

[MonetteDevilleDupont07]

Constraint

$𝚍𝚒𝚜𝚓 (𝚃𝙰𝚂𝙺𝚂)$

Argument

𝚃𝙰𝚂𝙺𝚂

𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (\begin{matrix} 𝚜𝚝𝚊𝚛𝚝 - 𝚍𝚟𝚊𝚛, \\ 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 𝚍𝚟𝚊𝚛, \\ 𝚋𝚎𝚏𝚘𝚛𝚎 - 𝚜𝚟𝚊𝚛, \\ 𝚙𝚘𝚜𝚒𝚝𝚒𝚘𝚗 - 𝚍𝚟𝚊𝚛 \end{matrix})

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚃𝙰𝚂𝙺𝚂, [𝚜𝚝𝚊𝚛𝚝, 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗, 𝚋𝚎𝚏𝚘𝚛𝚎, 𝚙𝚘𝚜𝚒𝚝𝚒𝚘𝚗])

𝚃𝙰𝚂𝙺𝚂 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 \geq 1

𝚃𝙰𝚂𝙺𝚂 . 𝚙𝚘𝚜𝚒𝚝𝚒𝚘𝚗 \geq 0

𝚃𝙰𝚂𝙺𝚂 . 𝚙𝚘𝚜𝚒𝚝𝚒𝚘𝚗 < | 𝚃𝙰𝚂𝙺𝚂 |

Purpose

All the tasks of the collection $𝚃𝙰𝚂𝙺𝚂$ should not overlap. For a given task $t$ the attributes $𝚋𝚎𝚏𝚘𝚛𝚎$ and $𝚙𝚘𝚜𝚒𝚝𝚒𝚘𝚗$ respectively correspond to the set of tasks starting before task $t$ (assuming that the first task is labelled by 1) and to the position of task $t$ (assuming that the first task has position 0).

Example

(\begin{matrix} 〈\begin{matrix} 𝚜𝚝𝚊𝚛𝚝 - 1 & 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 3 & 𝚋𝚎𝚏𝚘𝚛𝚎 - \emptyset & 𝚙𝚘𝚜𝚒𝚝𝚒𝚘𝚗 - 0, \\ 𝚜𝚝𝚊𝚛𝚝 - 9 & 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 1 & 𝚋𝚎𝚏𝚘𝚛𝚎 - {1, 3, 4} & 𝚙𝚘𝚜𝚒𝚝𝚒𝚘𝚗 - 3, \\ 𝚜𝚝𝚊𝚛𝚝 - 7 & 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 2 & 𝚋𝚎𝚏𝚘𝚛𝚎 - {1, 4} & 𝚙𝚘𝚜𝚒𝚝𝚒𝚘𝚗 - 2, \\ 𝚜𝚝𝚊𝚛𝚝 - 4 & 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 - 1 & 𝚋𝚎𝚏𝚘𝚛𝚎 - {1} & 𝚙𝚘𝚜𝚒𝚝𝚒𝚘𝚗 - 1 \end{matrix}〉 \end{matrix})

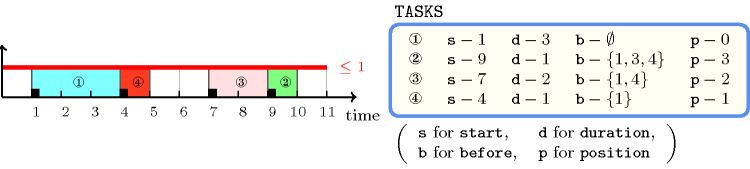
Figure 5.122.1 shows the tasks of the example. Since these tasks do not overlap the $𝚍𝚒𝚜𝚓$ constraint holds.

Figure 5.122.1. Tasks corresponding to the Example slot

Typical

| 𝚃𝙰𝚂𝙺𝚂 | > 1

Symmetries

One and the same constant can be added to the $𝚜𝚝𝚊𝚛𝚝$ attribute of all items of $𝚃𝙰𝚂𝙺𝚂$ .
$𝚃𝙰𝚂𝙺𝚂 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗$ can be decreased to any value $\geq 1$ .

Usage

The $𝚍𝚒𝚜𝚓$ constraint was originally applied [MonetteDevilleDupont07] to solve the open-shop problem.

Remark

This constraint is similar to the $𝚍𝚒𝚜𝚓𝚞𝚗𝚌𝚝𝚒𝚟𝚎$ constraint. In addition to the $𝚜𝚝𝚊𝚛𝚝$ and the $𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗$ attributes of a task $t$ , the $𝚍𝚒𝚜𝚓$ constraint introduces a set variable $𝚋𝚎𝚏𝚘𝚛𝚎$ that represents the set of tasks that end before the start of task $t$ as well as a domain variable $𝚙𝚘𝚜𝚒𝚝𝚒𝚘𝚗$ that gives the absolute order of task $t$ in the resource. Since it assumes that the first task has position 0 we have that, for a given task $t$ , the number of elements of its $𝚋𝚎𝚏𝚘𝚛𝚎$ attribute is equal to the value of its $𝚙𝚘𝚜𝚒𝚝𝚒𝚘𝚗$ attribute.

Algorithm

The main idea of the algorithm is to apply in a systematic way shaving on the $𝚙𝚘𝚜𝚒𝚝𝚒𝚘𝚗$ attribute of a task. It is implemented in Gecode [Gecode06].

used in graph description: $𝚒𝚗_𝚜𝚎𝚝$ .

Keywords

complexity: sequencing with release times and deadlines.

constraint arguments: constraint involving set variables.

constraint type: scheduling constraint, resource constraint, decomposition.

Arc input(s)

$𝚃𝙰𝚂𝙺𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

(\neq) \mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚝𝚊𝚜𝚔𝚜 1, 𝚝𝚊𝚜𝚔𝚜 2)

Arc arity

Arc constraint(s)

• ⋁ (\begin{matrix} 𝚝𝚊𝚜𝚔𝚜 1 . 𝚜𝚝𝚊𝚛𝚝 + 𝚝𝚊𝚜𝚔𝚜 1 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 \leq 𝚝𝚊𝚜𝚔𝚜 2 . 𝚜𝚝𝚊𝚛𝚝, \\ 𝚝𝚊𝚜𝚔𝚜 2 . 𝚜𝚝𝚊𝚛𝚝 + 𝚝𝚊𝚜𝚔𝚜 2 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 \leq 𝚝𝚊𝚜𝚔𝚜 1 . 𝚜𝚝𝚊𝚛𝚝 \end{matrix})

• \begin{matrix} 𝚝𝚊𝚜𝚔𝚜 1 . 𝚜𝚝𝚊𝚛𝚝 + 𝚝𝚊𝚜𝚔𝚜 1 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 \leq 𝚝𝚊𝚜𝚔𝚜 2 . 𝚜𝚝𝚊𝚛𝚝 \Leftrightarrow \\ 𝚒𝚗_𝚜𝚎𝚝 (𝚝𝚊𝚜𝚔𝚜 1 . 𝚔𝚎𝚢, 𝚝𝚊𝚜𝚔𝚜 2 . 𝚋𝚎𝚏𝚘𝚛𝚎) \end{matrix}

• \begin{matrix} 𝚝𝚊𝚜𝚔𝚜 1 . 𝚜𝚝𝚊𝚛𝚝 + 𝚝𝚊𝚜𝚔𝚜 1 . 𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗 \leq 𝚝𝚊𝚜𝚔𝚜 2 . 𝚜𝚝𝚊𝚛𝚝 \Leftrightarrow \\ 𝚝𝚊𝚜𝚔𝚜 1 . 𝚙𝚘𝚜𝚒𝚝𝚒𝚘𝚗 < 𝚝𝚊𝚜𝚔𝚜 2 . 𝚙𝚘𝚜𝚒𝚝𝚒𝚘𝚗 \end{matrix}

Graph property(ies)

𝐍𝐀𝐑𝐂

= | 𝚃𝙰𝚂𝙺𝚂 | * | 𝚃𝙰𝚂𝙺𝚂 | - | 𝚃𝙰𝚂𝙺𝚂 |

Graph model

We generate a clique with a non-overlapping constraint between each pair of distinct tasks and state that the number of arcs of the final graph should be equal to the number of arcs of the initial graph. For two tasks $t_{1}$ and $t_{2}$ , the three conditions of the arc constraint respectively correspond to:

The fact that $t_{1}$ ends before the start of $t_{2}$ or that $t_{2}$ ends before the start of $t_{1}$ .
The equivalence between the fact that $t_{1}$ ends before the start of $t_{2}$ and the fact that the identifier of task $t_{1}$ belongs to the $𝚋𝚎𝚏𝚘𝚛𝚎$ attribute of task $t_{2}$ .
The equivalence between the fact that $t_{1}$ ends before the start of $t_{2}$ and the fact that the $𝚙𝚘𝚜𝚒𝚝𝚒𝚘𝚗$ attribute of task $t_{1}$ is strictly less than the $𝚙𝚘𝚜𝚒𝚝𝚒𝚘𝚗$ attribute of task $t_{2}$ .

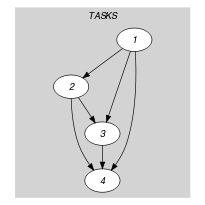
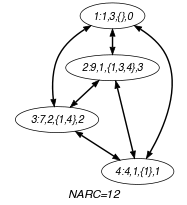
Parts (A) and (B) of Figure 5.122.2 respectively show the initial and final graph associated with the Example slot. The $𝚍𝚒𝚜𝚓$ constraint holds since all the arcs of the initial graph belong to the final graph: all the non-overlapping constraints holds.

Figure 5.122.2. Initial and final graph of the $𝚍𝚒𝚜𝚓$ constraint


(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.122. disj

Figure 5.122.1. Tasks corresponding to the Example slot

Figure 5.122.2. Initial and final graph of the 𝚍𝚒𝚜𝚓 constraint

Figure 5.122.2. Initial and final graph of the $𝚍𝚒𝚜𝚓$ constraint