5.263. minimum_except_0
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
All variables of the collection are assigned a value that belongs to interval . is the minimum value of the collection of domain variables , ignoring all variables that take 0 as value. When all variables of the collection are assigned value 0, is set to the default value .
- Example
-
The three examples of the constraint respectively hold since:
Within the first example, is set to the minimum value 3 of the collection .
Within the second example, is set to the minimum value 2 (ignoring value 0) of the collection .
Finally within the third example, is set to the default value 1000000 since all items of the collection are set to 0.
- Typical
- Symmetries
Items of are permutable.
All occurrences of two distinct values of can be swapped.
- Arg. properties
Functional dependency: determined by and .
- Remark
The joker value 0 makes sense only because we restrict the variables of the collection to take non-negative values.
- Reformulation
By (1) associating to each variable of the collection a rank variable with the reified constraint , and by creating for each pair of variables the reified constraints
,
,
,
and by (2) creating the reified constraint
,
one can reformulate the constraint in term of reified constraints.
- See also
hard version: (value 0 is not ignored any more).
- Keywords
characteristic of a constraint: joker value, minimum, automaton, automaton without counters, reified automaton constraint.
constraint arguments: pure functional dependency.
constraint network structure: centered cyclic(1) constraint network(1).
- Cond. implications
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph property(ies)
-
- Graph model
Because of the first two conditions of the arc constraint, all vertices that correspond to 0 will be removed from the final graph.
Parts (A) and (B) of Figure 5.263.1 respectively show the initial and final graph of the second example of the Example slot. Since we use the graph property, the vertices of rank 0 (without considering the loops) of the final graph are outlined with a thick circle.
Figure 5.263.1. Initial and final graph of the constraint
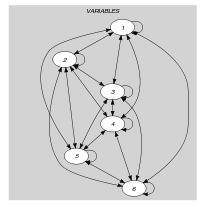
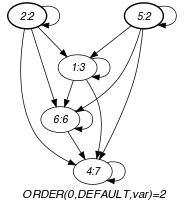
(a) (b) Since the graph associated with the third example does not contain any vertex, returns the default value .
- Automaton
Figure 5.263.2 depicts the automaton associated with the constraint. Let be the variable of the collection. To each pair corresponds a signature variable as well as the following signature constraint:
.
Figure 5.263.2. Automaton of the constraint
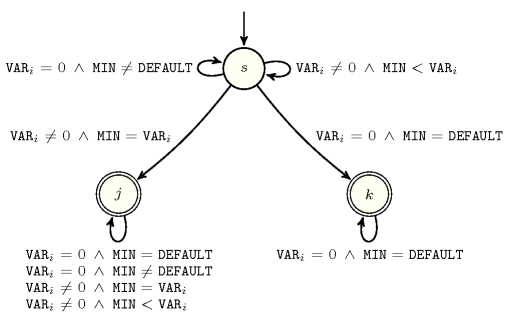
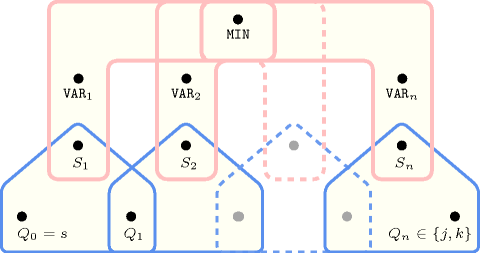
Figure 5.263.3. Hypergraph of the reformulation corresponding to the automaton of the constraint