5.329. proper_forest
| DESCRIPTION | LINKS | GRAPH |
- Origin
Derived from , [BeldiceanuKatrielLorca06].
- Constraint
- Arguments
- Restrictions
- Purpose
Cover an undirected graph by a set of trees (i.e., a tree is a connected graph without cycles that contains at least two vertices [Cayley89]) in such a way that each vertex of belongs to one distinct tree.
- Example
-
The constraint holds since the undirected graph associated with the items of the collection corresponds to a forest containing trees: each tree respectively involves the vertices , and .
- Typical
- Symmetry
Items of are permutable.
- Arg. properties
Functional dependency: determined by .
- Algorithm
A filtering algorithm for the constraint was proposed by N. Beldiceanu et al. in [BeldiceanuKatrielLorca06]. It achieves hybrid-consistency and its running time is dominated by the complexity of finding all edges that do not belong to any maximum cardinality matching in an undirected -vertex, -edge graph, i.e., .
- Systems
- See also
- Keywords
characteristic of a constraint: undirected graph.
constraint arguments: constraint involving set variables.
constraint type: graph constraint.
filtering: hybrid-consistency.
final graph structure: connected component, tree, no cycle, symmetric.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph class
-
- Graph model
The graph constraint forces the following conditions:
Each connected component of the final graph has vertices and arcs. This is equivalent to the fact that each connected component has not any cycle.
Since we use the arc-generator and since, by definition, the final graph does not contain any isolated vertex, each connected component of the final graph involves more than one vertex.
The number of connected components of the final graph is equal to .
All the vertices of the initial graph belong to the final graph.
The final graph is symmetric.
Parts (A) and (B) of Figure 5.329.1 respectively show the initial and final graph associated with the Example slot. For each connected component we display its number of arcs as well as its number of vertices. The constraint holds since the final graph has connected components and no cycle.
Figure 5.329.1. Initial and final graph of the constraint
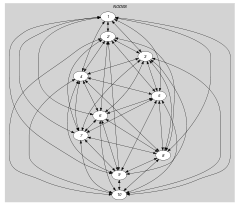
(a) 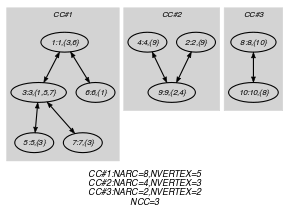
(b)