Global Constraint Catalog: Csoft_all_equal_min

5.357. soft_all_equal_min_ctr

DESCRIPTION

LINKS

GRAPH

Origin

[HebrardSullivanRazgon08]

Constraint

$𝚜𝚘𝚏𝚝_𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚖𝚒𝚗_𝚌𝚝𝚛 (𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂)$

Synonyms

$𝚜𝚘𝚏𝚝_𝚊𝚕𝚕𝚍𝚒𝚏𝚏_𝚖𝚊𝚡_𝚌𝚝𝚛$ , $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚖𝚊𝚡_𝚌𝚝𝚛$ , $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝_𝚖𝚊𝚡_𝚌𝚝𝚛$ .

Arguments

$𝙽$	$𝚒𝚗𝚝$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝙽 \geq 0

𝙽 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | * | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

Purpose

Consider the equality constraints involving two distinct variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ . Among the previous set of constraints, $𝙽$ is less than or equal to the number of equality constraints that hold.

Example

(6, 〈5, 1, 5, 5〉)

Within the collection $〈 5, 1, 5, 5 〉$ six equality constraints holds. Consequently, the $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚌𝚝𝚛$ constraint holds since the argument $𝙽 = 6$ is less than or equal to the number of equality constraints that hold.

Typical

𝙽 > 0

𝙽 < | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | * | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | - | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

Symmetries

$𝙽$ can be decreased to any value $\geq 0$ .
Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are permutable.
All occurrences of two distinct values of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ can be swapped; all occurrences of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ can be renamed to any unused value.

Remark

It was shown in [HebrardSullivanRazgon08] that, finding out whether the $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚌𝚝𝚛$ constraint has a solution or not is NP-hard. This was achieved by reduction from 3-dimensional-matching. Hebrard et al. also identify a tractable class when no value occurs in more than two variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ that is equivalent to the vertex matching problem. One year later, [HebrardMarxSullivanRazgon09] shows how to achieve bound-consistency in polynomial time.

hard version: $𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕$ .

implied by: $𝚊𝚗𝚍$ , $𝚋𝚊𝚕𝚊𝚗𝚌𝚎$ , $𝚎𝚚𝚞𝚒𝚟𝚊𝚕𝚎𝚗𝚝$ , $𝚗𝚘𝚛$ .

related: $𝚊𝚝𝚖𝚘𝚜𝚝_𝚗𝚟𝚊𝚕𝚞𝚎$ .

Keywords

complexity: 3-dimensional-matching.

constraint type: soft constraint, value constraint, relaxation, decomposition-based violation measure.

filtering: bound-consistency.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

(\neq) \mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 = 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛

Graph property(ies)

𝐍𝐀𝐑𝐂

\geq 𝙽

Graph model

We generate an initial graph with binary equalities constraints between each vertex and its successors. We use the arc generator $𝐶𝐿𝐼𝑄𝑈𝐸 (\neq)$ in order to avoid considering equality constraints between the same variable. The graph property states that $𝙽$ is less than or equal to the number of equalities that hold in the final graph.

Parts (A) and (B) of Figure 5.357.1 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐀𝐑𝐂$ graph property, the arcs of the final graph are stressed in bold. Six equality constraints remain in the final graph.

Figure 5.357.1. Initial and final graph of the $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚖𝚒𝚗_𝚌𝚝𝚛$ constraint


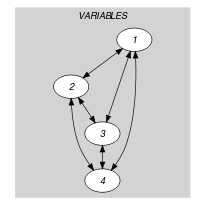
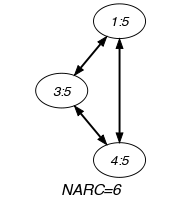
(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.357. soft_all_equal_min_ctr

Figure 5.357.1. Initial and final graph of the 𝚜𝚘𝚏𝚝_𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚖𝚒𝚗_𝚌𝚝𝚛 constraint

Figure 5.357.1. Initial and final graph of the $𝚜𝚘𝚏𝚝_𝚊𝚕𝚕_𝚎𝚚𝚞𝚊𝚕_𝚖𝚒𝚗_𝚌𝚝𝚛$ constraint