5.333. roots
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
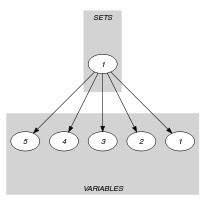
is the set of indices of the variables in the collection taking their values in ; . Positions are numbered from 1.
- Example
-
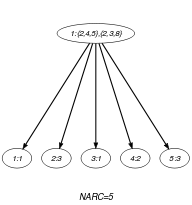
The constraint holds since values 2 and 3 in occur in the collection only at positions . The value does not occur within the collection .
- Typical
- Usage
Bessière et al. showed [BessiereHebrardHnichKiziltanWalsh05IJCAI] that many counting and occurence constraints can be specified with two global primitives: and . For instance, the constraint can be decomposed into one constraint: iff .
does not count but collects the set of variables using particular values. It provides then a way of channeling. generalises, for instance, the constraint, iff , or may be used instead of the .
Other examples of reformulations are given in [BessiereHebrardHnichKiziltanWalsh09].
- Algorithm
In [BessiereHebrardHnichKiziltanWalsh06CP], Bessière et al. shows that enforcing hybrid-consistency on is NP-hard. They consider the decomposition of into a network of ternary constraints: , and . Enforcing bound consistency on the decomposition achieves bound consistency on . Enforcing hybrid consistency on the decomposition achieves at least bound consistency on , until hybrid consistency in some special cases:
,
,
are ground,
is ground.
Enforcing hybrid consistency on the decomposition can be done in with and the maximum domain size of and .
- Systems
- See also
common keyword: (constraint involving set variables).
related: (can be expressed with ), (can be expressed with and ), , (can be expressed with ), (can be expressed with and ), (can be expressed with ), , , (can be expressed with ), , (can be expressed with and ).
- Keywords
characteristic of a constraint: disequality.
constraint arguments: constraint involving set variables.
constraint type: counting constraint, value constraint, decomposition.
- Derived Collection