5.126. disjunctive
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Synonym
.
- Argument
- Restrictions
- Purpose
All the tasks of the collection that have a duration strictly greater than 0 should not overlap.
- Example
-
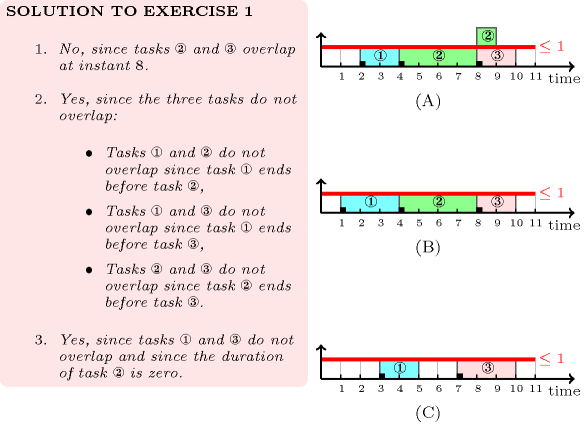
Figure 5.126.1 shows the tasks with non-zero duration of the example. Since these tasks do not overlap the constraint holds.
Figure 5.126.1. Tasks with non-zero duration of the Example slot

- All solutions
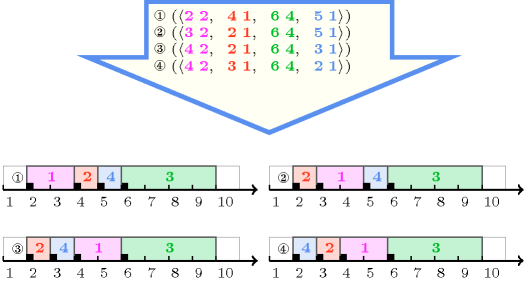
Figure 5.126.2 gives all solutions to the following non ground instance of the constraint: , , , , , , , , .
Figure 5.126.2. All solutions corresponding to the non ground example of the constraint of the All solutions slot
- Typical
- Symmetries
Items of are permutable.
can be decreased to any value .
One and the same constant can be added to the attribute of all items of .
- Arg. properties
Contractible wrt. .
- Usage
The constraint occurs in many resource scheduling problems in order to model a resource that can not be shared. This means that tasks using this resource can not overlap in time. Quite often constraints are used together with precedence constraints. A precedence constraint between two tasks models the fact that the processing of a task has to be postponed until an other task is completed. Such mix of disjunctive and precedence constraints occurs for instance in job-shop problems.
- Remark
Some systems like Ilog CP Optimizer also imposes that zero duration tasks do not overlap non-zero duration tasks.
A soft version of this constraint, under the hypothesis that all durations are fixed, was presented by P. Baptiste et al. in [BaptisteLePapePeridy98]. In this context the goal was to perform as many tasks as possible within their respective due-dates.
When all tasks have the same (fixed) duration the constraint can be reformulated as an constraint for which a filtering algorithm achieving bound-consistency is available [ArtiouchineBaptiste05].
Within the context of linear programming [Hooker07book] provides several relaxations of the constraint.
Some solvers use in a pre-processing phase, while stating precedence and cumulative constraints, an algorithm for automatically extracting large cliques [BronKerbosch73] from a set of tasks that should not pairwise overlap (i.e., two tasks and can not overlap either, because ends before the start of , either because the sum of resource consumption of and exceeds the capacity of a cumulative resource that both tasks use) in order to state constraints.
- Algorithm
We have four main families of methods for handling the constraint:
Methods based on the compulsory part [Lahrichi82] of the tasks (also called time-tabling methods). These methods determine the time slots which for sure are occupied by a given task, an propagate back this information to the attributes of each task (i.e., the origin and the duration). Because of their simplicity, these methods have been originally used for handling the constraint. Even if they propagate less than the other methods they can in practice handle a large number of tasks. To our best knowledge no efficient incremental algorithm devoted to this problem was published up to now (i.e., September 2006).
Methods based on constructive disjunction. The idea is to try out each alternative of a disjunction (e.g., given two tasks and that should not overlap, we successively assume that finishes before , and that finishes before ) and to remove values that were pruned in both alternatives.
Methods based on edge-finding. Given a set of tasks , edge-finding determines that some task must, can, or cannot execute first or last in . Efficient edge-finding algorithms for handling the constraint were originally described in [CarlierPinson88], [CarlierPinson90] and more recently in [Vilim04], [PeridyRivreau05].
Methods that, for any task , consider the maximal number of tasks that can end up before the start of task as well as the maximal number of tasks that can start after the end of task [Wolf05].
All these methods are usually used for adjusting the minimum and maximum values of the variables of the constraint. However some systems use these methods for pruning the full domain of the variables. Finally, Jackson priority rule [Jackson55] provides a necessary condition [CarlierPinson90] for the constraint. Given a set of tasks , it consists to progressively schedule all tasks of in the following way:
It assigns to the first possible time point (i.e., the earliest start of all tasks of ) the available task with minimal latest end. In this context, available means a task for which the earliest start is less than or equal to the considered time point.
It continues by considering the next time point until all the tasks are completely scheduled.
- Systems
disjunctive in Choco, unary in Gecode.
- See also
common keyword: , , , (scheduling constraint).
generalisation: ( and are not necessarly all equal to 1), ( of 1 replaced by orthotope).
implies: , .
specialisation: ( replaced by , of same length), ( replaced by ).
- Keywords
characteristic of a constraint: core, sort based reformulation.
complexity: sequencing with release times and deadlines.
constraint type: scheduling constraint, resource constraint, decomposition.
filtering: compulsory part, constructive disjunction, Phi-tree.
modelling: disjunction, sequence dependent set-up, zero-duration task.
- Cond. implications
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
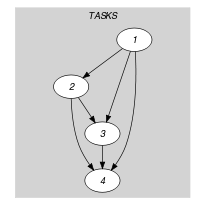
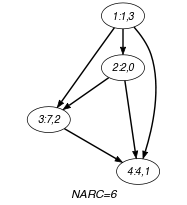
We generate a clique with a non-overlapping constraint between each pair of distinct tasks and state that the number of arcs of the final graph should be equal to the number of arcs of the initial graph.
Parts (A) and (B) of Figure 5.126.3 respectively show the initial and final graph associated with the Example slot. The constraint holds since all the arcs of the initial graph belong to the final graph: all the non-overlapping constraints holds.
Figure 5.126.3. Initial and final graph of the constraint
(a) (b) - Quiz
: checking whether a ground instance holds or not