5.58. cardinality_atleast
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
is the minimum number of time that a value of is taken by the variables of the collection .
- Example
-
In this example, values 3 and 8 are respectively used 2, and 1 times. The constraint holds since its first argument is assigned to the minimum number of time that values 3 and 8 occur in the collection .
- Typical
- Symmetries
Items of are permutable.
Items of are permutable.
An occurrence of a value of that does not belong to can be replaced by any other value that also does not belong to .
All occurrences of two distinct values in or can be swapped; all occurrences of a value in or can be renamed to any unused value.
- Arg. properties
Functional dependency: determined by and .
- Usage
An application of the constraint is to enforce a minimum use of values.
- Remark
This is a restricted form of a variant of an constraint and of the constraint. In the original constraint, one specifies for each value its minimum and maximum number of occurrences.
- Algorithm
See [Regin96].
- See also
generalisation: (single replaced by an individual for each value).
- Keywords
-
characteristic of a constraint: automaton, automaton with array of counters.
constraint arguments: pure functional dependency.
constraint type: value constraint.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph class
-
- Graph model
Using directly the graph property , and replacing the disequality of the arc constraint by an equality does not work since it ignores values that are not assigned to any variable. This comes from the fact that isolated vertices are removed from the final graph.
Parts (A) and (B) of Figure 5.58.1 respectively show the initial and final graph associated with the Example slot. Since we use the graph property, the vertex with the maximum number of predecessor (i.e., namely two predecessors) is stressed with a double circle. As a consequence the first argument of the constraint is assigned to the total number of variables 3 minus 2.
Figure 5.58.1. Initial and final graph of the constraint
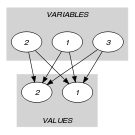
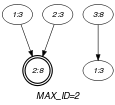
(a) (b)
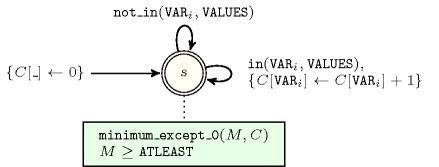
- Automaton
Figure 5.58.2 depicts the automaton associated with the constraint. To each variable of the collection corresponds a 0-1 signature variable . The following signature constraint links and : .
Figure 5.58.2. Automaton of the constraint