Global Constraint Catalog: Cdisjoint

5.123. disjoint

DESCRIPTION

LINKS

GRAPH

AUTOMATON

Origin

Derived from $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ .

Constraint

$𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝 (𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2)$

Arguments

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚟𝚊𝚛)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2, 𝚟𝚊𝚛)

Purpose

Each variable of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ should take a value that is distinct from all the values assigned to the variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ .

Example

(〈1, 9, 1, 5〉, 〈2, 7, 7, 0, 6, 8〉)

In this example, values $1, 5, 9$ are used by the variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ and values $0, 2, 6, 7, 8$ by the variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ . Since there is no intersection between the two previous sets of values the $𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝$ constraint holds.

All solutions

Figure 5.123.1 gives all solutions to the following non ground instance of the $𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝$ constraint: $U_{1} \in [0 . . 2]$ , $U_{2} \in [1 . . 2]$ , $U_{3} \in [1 . . 2]$ , $V_{1} \in [0 . . 1]$ , $V_{2} \in [1 . . 2]$ , $𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝$ $(〈 U_{1}, U_{2}, U_{3} 〉, 〈 V_{1}, V_{2} 〉)$ .

Figure 5.123.1. All solutions corresponding to the non ground example of the $𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝$ constraint of the All solutions slot

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | > 1

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 | > 1

Symmetries

Arguments are permutable w.r.t. permutation $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2)$ .
Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ are permutable.
Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ are permutable.
An occurrence of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛$ can be replaced by any value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛$ .
An occurrence of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛$ can be replaced by any value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛$ .
All occurrences of two distinct values in $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛$ or $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛$ can be swapped; all occurrences of a value in $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛$ or $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛$ can be renamed to any unused value.

Arg. properties

Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ .
Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ .

Remark

Despite the fact that this is not an uncommon constraint, it can not be modelled in a compact way neither with a disequality constraint (i.e., two given variables have to take distinct values) nor with the $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ constraint. The $𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝$ constraint can bee seen as a special case of the $𝚌𝚘𝚖𝚖𝚘𝚗$ $(𝙽𝙲𝙾𝙼𝙼𝙾𝙽 1, 𝙽𝙲𝙾𝙼𝙼𝙾𝙽 2, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2)$ constraint where $𝙽𝙲𝙾𝙼𝙼𝙾𝙽 1$ and $𝙽𝙲𝙾𝙼𝙼𝙾𝙽 2$ are both set to 0.

MiniZinc (http://www.minizinc.org/) has a $𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝$ constraint between two set variables rather than between two collections of variables.

Algorithm

Let us note:

$n_{1}$ the minimum number of distinct values taken by the variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ .
$n_{2}$ the minimum number of distinct values taken by the variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ .
$n_{12}$ the maximum number of distinct values taken by the union of the variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ and $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ .

One invariant to maintain for the $𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝$ constraint is $n_{1} + n_{2} \leq n_{12}$ . A lower bound of $n_{1}$ and $n_{2}$ can be obtained by using the algorithms provided in [Beldiceanu01], [BeldiceanuCarlssonThiel02]. An exact upper bound of $n_{12}$ can be computed by using a bipartite matching algorithm.

Used in

$𝚔_𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝$ .

See also

generalisation: $𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝_𝚝𝚊𝚜𝚔𝚜$ ( $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ replaced by $𝚝𝚊𝚜𝚔$ ).

implies: $𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚘𝚗_𝚒𝚗𝚝𝚎𝚛𝚜𝚎𝚌𝚝𝚒𝚘𝚗$ , $𝚕𝚎𝚡_𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ .

system of constraints: $𝚔_𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝$ .

Keywords

characteristic of a constraint: disequality, automaton, automaton with array of counters.

constraint type: value constraint.

filtering: bipartite matching.

modelling: empty intersection.

Arc input(s): $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$
Arc generator: $𝑃𝑅𝑂𝐷𝑈𝐶𝑇$ $\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)$
Arc arity
Arc constraint(s): $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 = 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛$
Graph property(ies): $𝐍𝐀𝐑𝐂$ $= 0$
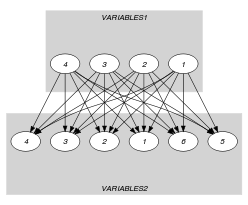
Graph model: $𝑃𝑅𝑂𝐷𝑈𝐶𝑇$ is used in order to generate the arcs of the graph between all variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ and all variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ . Since we use the graph property $𝐍𝐀𝐑𝐂$ $=$ 0 the final graph will be empty. Figure 5.123.2 shows the initial graph associated with the Example slot. Since we use the $𝐍𝐀𝐑𝐂$ $=$ 0 graph property the final graph is empty.

Figure 5.123.2. Initial graph of the $𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝$ constraint (the final graph is empty)
Signature: Since 0 is the smallest number of arcs of the final graph we can rewrite $𝐍𝐀𝐑𝐂$ $=$ 0 to $𝐍𝐀𝐑𝐂$ $\leq$ 0. This leads to simplify $\underset{̲}{\bar{𝐍𝐀𝐑𝐂}}$ to $\underset{̲}{𝐍𝐀𝐑𝐂}$ .

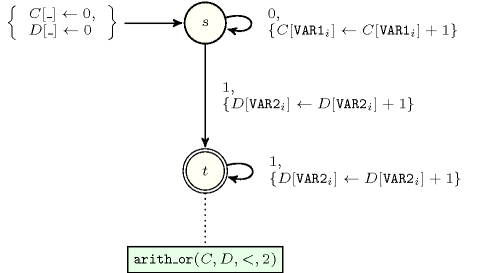
Automaton: Figure 5.123.3 depicts the automaton associated with the $𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝$ constraint. To each variable $𝚅𝙰𝚁 1_{i}$ of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ corresponds a signature variable $S_{i}$ that is equal to 0. To each variable $𝚅𝙰𝚁 2_{i}$ of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ corresponds a signature variable $S_{i + | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 |}$ that is equal to 1.

Figure 5.123.3. Automaton of the $𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2)$ constraint, where state $s$ handles variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ and state $t$ handles variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$

Global Constraint Catalog

5. Global Constraint Catalogue

5.123. disjoint

Figure 5.123.1. All solutions corresponding to the non ground example of the $𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝$ constraint of the All solutions slot

Figure 5.123.2. Initial graph of the $𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝$ constraint (the final graph is empty)

Global Constraint Catalog

5. Global Constraint Catalogue

5.123. disjoint

Figure 5.123.1. All solutions corresponding to the non ground example of the 𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝 constraint of the All solutions slot

Figure 5.123.2. Initial graph of the 𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝 constraint (the final graph is empty)

Figure 5.123.1. All solutions corresponding to the non ground example of the $𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝$ constraint of the All solutions slot

Figure 5.123.2. Initial graph of the $𝚍𝚒𝚜𝚓𝚘𝚒𝚗𝚝$ constraint (the final graph is empty)