5.234. link_set_to_booleans
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
Make the link between a set variable and those 0-1 variables that are associated with each potential value belonging to : The 0-1 variables, which are associated with a value belonging to the set variable , are equal to 1, while the remaining 0-1 variables are all equal to 0.
- Example
-
In the example, the 0-1 variables associated with the values 1, 3 and 4 are all set to 1, while the other 0-1 variables are set to 0. Consequently, the constraint holds since its first argument is set to .
- Typical
- Symmetry
Items of are permutable.
- Usage
This constraint is used in order to make the link between a formulation using set variables and a formulation based on linear programming.
- Systems
channel in Gecode, link_set_to_booleans in MiniZinc.
- See also
common keyword: , (constraint involving set variables), (channelling constraint), , , , , , , (constraint involving set variables).
- Keywords
characteristic of a constraint: derived collection.
constraint arguments: constraint involving set variables.
constraint type: decomposition, value constraint.
- Derived Collection
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph model
The constraint is modelled with the following bipartite graph. The first set of vertices corresponds to a single vertex containing the set variable. The second class of vertices contains one vertex for each item of the collection . The arc constraint between the set variable and one potential value of the set variable expresses the following:
If the 0-1 variable associated with is equal to 1 then should belong to .
Otherwise if the 0-1 variable associated with is equal to 0 then should not belong to .
Since all arc constraints should hold the final graph contains exactly arcs.
Parts (A) and (B) of Figure 5.234.1 respectively show the initial and final graph associated with the Example slot. Since we use the graph property, the arcs of the final graph are stressed in bold. The constraint holds since the final graph contains exactly 6 arcs (one for each 0-1 variable).
Figure 5.234.1. Initial and final graph of the constraint
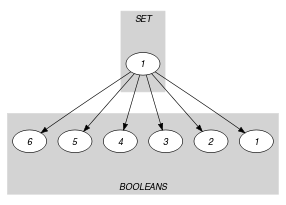
(a) 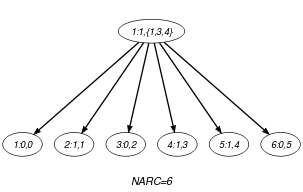
(b) - Signature
Since the initial graph contains arcs the maximum number of arcs of the final graph is equal to . Therefore we can rewrite the graph property to and simplify to .