5.41. atmost_nvalue
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Synonyms
, , .
- Arguments
- Restrictions
- Purpose
The number of distinct values taken by the variables of the collection is less than or equal to .
- Example
-
The first constraint holds since the collection involves at most 4 distinct values (i.e., in fact 3 distinct values).
- Typical
- Symmetries
can be increased.
Items of are permutable.
All occurrences of two distinct values of can be swapped; all occurrences of a value of can be renamed to any unused value.
An occurrence of a value of can be replaced by any value of .
- Arg. properties
Contractible wrt. .
- Remark
This constraint was introduced together with the constraint by C. Bessière et al. in an article [BessiereHebrardHnichKiziltanWalsh05] providing filtering algorithms for the constraint.
It was shown in [BessiereHebrardHnichWalshO4] that, finding out whether a constraint has a solution or not is NP-hard. This was achieved by reduction from 3-SAT.
- Algorithm
[Beldiceanu01] provides an algorithm that achieves bound consistency. [BeldiceanuCarlssonThiel02] provides two filtering algorithms, while [BessiereHebrardHnichKiziltanWalsh05] provides a greedy algorithm and a graph invariant for evaluating the minimum number of distinct values. [BessiereHebrardHnichKiziltanWalsh05] also gives a linear relaxation for approximating the minimum number of distinct values.
- Counting
-
Length () 2 3 4 5 6 7 8 Solutions 12 108 1280 18750 326592 6588344 150994944 Number of solutions for : domains
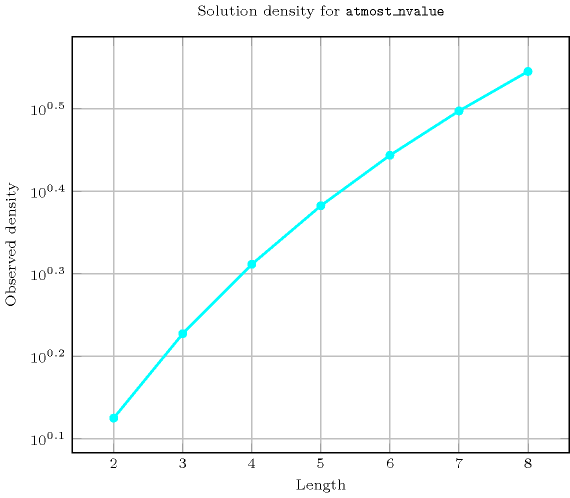
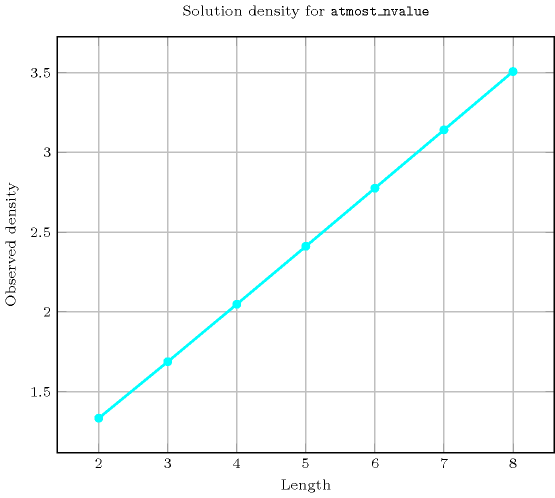
Length () 2 3 4 5 6 7 8 Total 12 108 1280 18750 326592 6588344 150994944 Parameter value 1 3 4 5 6 7 8 9 2 9 40 145 456 1309 3536 9153 3 - 64 505 3456 20209 104672 496017 4 - - 625 7056 74809 692672 5639841 5 - - - 7776 112609 1633472 21515841 6 - - - - 117649 2056832 37603521 7 - - - - - 2097152 42683841 8 - - - - - - 43046721 Solution count for : domains
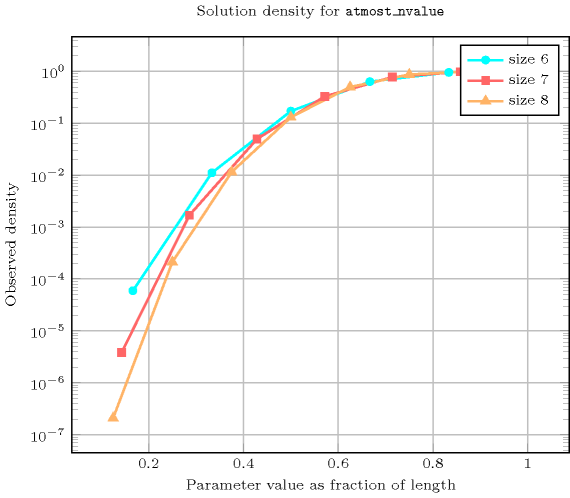
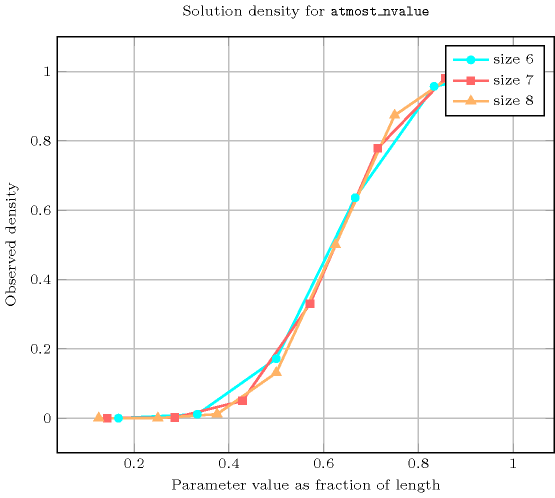
- Systems
atMostNValue in Choco.
- See also
-
implied by: ( replaced by ).
related: , , , , .
- Keywords
-
constraint type: counting constraint, value partitioning constraint.
final graph structure: strongly connected component, equivalence.
modelling: number of distinct equivalence classes, number of distinct values.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Graph class
-
- Graph model
Parts (A) and (B) of Figure 5.41.1 respectively show the initial and final graph associated with the first example of the Example slot. Since we use the graph property we show the different strongly connected components of the final graph. Each strongly connected component corresponds to a specific value that is assigned to some variables of the collection. The 3 following values 1, 3 and 6 are used by the variables of the collection.
Figure 5.41.1. Initial and final graph of the constraint
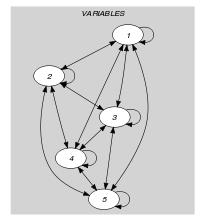
(a) 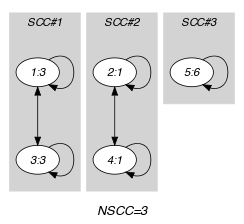
(b)