Global Constraint Catalog: Copen

5.296. open_atleast

DESCRIPTION

LINKS

GRAPH

Origin

Derived from $𝚊𝚝𝚕𝚎𝚊𝚜𝚝$ and $𝚘𝚙𝚎𝚗_𝚐𝚕𝚘𝚋𝚊𝚕_𝚌𝚊𝚛𝚍𝚒𝚗𝚊𝚕𝚒𝚝𝚢$ .

Constraint

$𝚘𝚙𝚎𝚗_𝚊𝚝𝚕𝚎𝚊𝚜𝚝 (𝚂, 𝙽, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚅𝙰𝙻𝚄𝙴)$

Arguments

$𝚂$	$𝚜𝚟𝚊𝚛$
$𝙽$	$𝚒𝚗𝚝$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚅𝙰𝙻𝚄𝙴$	$𝚒𝚗𝚝$

Restrictions

𝚂 \geq 1

𝚂 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

𝙽 \geq 0

𝙽 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

Purpose

Let $𝒱$ be the variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ for which the corresponding position belongs to the set $𝚂$ . Positions are numbered from 1. At least $𝙽$ variables of $𝒱$ are assigned value $𝚅𝙰𝙻𝚄𝙴$ .

Example

({2, 3, 4}, 2, 〈4, 2, 4, 4〉, 4)

The $𝚘𝚙𝚎𝚗_𝚊𝚝𝚕𝚎𝚊𝚜𝚝$ constraint holds since, within the last three (i.e., $𝚂 = {2, 3, 4}$ ) values of the collection $〈 4, 2, 4, 4 〉$ , at least $𝙽 = 2$ values are equal to value $𝚅𝙰𝙻𝚄𝙴 = 4$ .

Typical

𝙽 > 0

𝙽 < | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

Symmetries

$𝙽$ can be decreased to any value $\geq 0$ .
An occurrence of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ that is different from $𝚅𝙰𝙻𝚄𝙴$ can be replaced by any other value.

Arg. properties

Suffix-extensible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ .

comparison swapped: $𝚘𝚙𝚎𝚗_𝚊𝚝𝚖𝚘𝚜𝚝$ .

hard version: $𝚊𝚝𝚕𝚎𝚊𝚜𝚝$ .

used in graph description: $𝚒𝚗_𝚜𝚎𝚝$ .

Keywords

constraint arguments: constraint involving set variables.

constraint type: open constraint, value constraint.

modelling: at least.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$

Arc generator

𝑆𝐸𝐿𝐹

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜)

Arc arity

Arc constraint(s)

• 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 . 𝚟𝚊𝚛 = 𝚅𝙰𝙻𝚄𝙴

•

𝚒𝚗_𝚜𝚎𝚝

(𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 . 𝚔𝚎𝚢, 𝚂)

Graph property(ies)

𝐍𝐀𝐑𝐂

\geq 𝙽

Graph model

Since each arc constraint involves only one vertex ( $𝚅𝙰𝙻𝚄𝙴$ is fixed), we employ the $𝑆𝐸𝐿𝐹$ arc generator in order to produce a graph with a single loop on each vertex. Variables for which the corresponding position does not belong to the set $𝚂$ are removed from the final graph by the second condition of the arc-constraint.

Parts (A) and (B) of Figure 5.296.1 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐀𝐑𝐂$ graph property, the loops of the final graph are stressed in bold.

Figure 5.296.1. Initial and final graph of the $𝚘𝚙𝚎𝚗_𝚊𝚝𝚕𝚎𝚊𝚜𝚝$ constraint


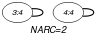
(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.296. open_atleast

Figure 5.296.1. Initial and final graph of the 𝚘𝚙𝚎𝚗_𝚊𝚝𝚕𝚎𝚊𝚜𝚝 constraint

Figure 5.296.1. Initial and final graph of the $𝚘𝚙𝚎𝚗_𝚊𝚝𝚕𝚎𝚊𝚜𝚝$ constraint