Global Constraint Catalog: Csymmetric

5.395. symmetric_alldifferent

DESCRIPTION

LINKS

GRAPH

Origin

[Regin99]

Constraint

$𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝 (𝙽𝙾𝙳𝙴𝚂)$

Synonyms

$𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚏𝚏$ , $𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝$ , $𝚜𝚢𝚖𝚖_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ , $𝚜𝚢𝚖𝚖_𝚊𝚕𝚕𝚍𝚒𝚏𝚏$ , $𝚜𝚢𝚖𝚖_𝚊𝚕𝚕𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝$ , $𝚘𝚗𝚎_𝚏𝚊𝚌𝚝𝚘𝚛$ , $𝚝𝚠𝚘_𝚌𝚢𝚌𝚕𝚎$ .

Argument

𝙽𝙾𝙳𝙴𝚂

𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚒𝚗𝚍𝚎𝚡 - 𝚒𝚗𝚝, 𝚜𝚞𝚌𝚌 - 𝚍𝚟𝚊𝚛)

Restrictions

| 𝙽𝙾𝙳𝙴𝚂 | \mod 2 = 0

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝙽𝙾𝙳𝙴𝚂, [𝚒𝚗𝚍𝚎𝚡, 𝚜𝚞𝚌𝚌])

𝙽𝙾𝙳𝙴𝚂 . 𝚒𝚗𝚍𝚎𝚡 \geq 1

𝙽𝙾𝙳𝙴𝚂 . 𝚒𝚗𝚍𝚎𝚡 \leq | 𝙽𝙾𝙳𝙴𝚂 |

𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝

(𝙽𝙾𝙳𝙴𝚂, 𝚒𝚗𝚍𝚎𝚡)

𝙽𝙾𝙳𝙴𝚂 . 𝚜𝚞𝚌𝚌 \geq 1

𝙽𝙾𝙳𝙴𝚂 . 𝚜𝚞𝚌𝚌 \leq | 𝙽𝙾𝙳𝙴𝚂 |

Purpose

All variables associated with the $𝚜𝚞𝚌𝚌$ attribute of the $𝙽𝙾𝙳𝙴𝚂$ collection should be pairwise distinct. In addition enforce the following condition: if variable $𝙽𝙾𝙳𝙴𝚂 [i] . 𝚜𝚞𝚌𝚌$ takes value $j$ with $j \neq i$ then variable $𝙽𝙾𝙳𝙴𝚂 [j] . 𝚜𝚞𝚌𝚌$ takes value $i$ . This can be interpreted as a graph-covering problem where one has to cover a digraph $G$ with circuits of length two in such a way that each vertex of $G$ belongs to a single circuit.

Example

(\begin{matrix} 〈\begin{matrix} 𝚒𝚗𝚍𝚎𝚡 - 1 & 𝚜𝚞𝚌𝚌 - 3, \\ 𝚒𝚗𝚍𝚎𝚡 - 2 & 𝚜𝚞𝚌𝚌 - 4, \\ 𝚒𝚗𝚍𝚎𝚡 - 3 & 𝚜𝚞𝚌𝚌 - 1, \\ 𝚒𝚗𝚍𝚎𝚡 - 4 & 𝚜𝚞𝚌𝚌 - 2 \end{matrix}〉 \end{matrix})

The $𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ constraint holds since:

$𝙽𝙾𝙳𝙴𝚂 [1] . 𝚜𝚞𝚌𝚌 = 3 \Leftrightarrow 𝙽𝙾𝙳𝙴𝚂 [3] . 𝚜𝚞𝚌𝚌 = 1$ ,
$𝙽𝙾𝙳𝙴𝚂 [2] . 𝚜𝚞𝚌𝚌 = 4 \Leftrightarrow 𝙽𝙾𝙳𝙴𝚂 [4] . 𝚜𝚞𝚌𝚌 = 2$ .

All solutions

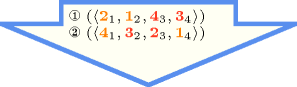
Figure 5.395.1 gives all solutions to the following non ground instance of the $𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ constraint: $S_{1} \in [1, 4]$ , $S_{2} \in [1, 3]$ , $S_{3} \in [1, 4]$ , $S_{4} \in [1, 3]$ , $𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ $(〈 1 S_{1}, 2 S_{2}, 3 S_{3}, 4 S_{4} 〉)$ .

Figure 5.395.1. All solutions corresponding to the non ground example of the $𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ constraint of the All solutions slot (the $𝚒𝚗𝚍𝚎𝚡$ attribute is displayed as indices of the $𝚜𝚞𝚌𝚌$ attribute)

Typical

| 𝙽𝙾𝙳𝙴𝚂 | \geq 4

Symmetry

Items of $𝙽𝙾𝙳𝙴𝚂$ are permutable.

Usage

As it was reported in [Regin99], this constraint is useful to express matches between persons or between teams. The $𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ constraint also appears implicitly in the cycle cover problem and corresponds to the four conditions given in section 1 Modeling the Cycle Cover Problem of [PesantSoriano98].

Remark

This constraint is referenced under the name $𝚘𝚗𝚎_𝚏𝚊𝚌𝚝𝚘𝚛$ in [HenzMullerThiel02] as well as in [Trick02]. From a modelling point of view this constraint can be expressed with the $𝚌𝚢𝚌𝚕𝚎$ constraint [BeldiceanuContejean94] where one imposes the additional condition that each cycle has only two nodes.

Algorithm

A filtering algorithm for the $𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ constraint was proposed by J.-C. Régin in [Regin99]. It achieves arc-consistency and its running time is dominated by the complexity of finding all edges that do not belong to any maximum cardinality matching in an undirected $n$ -vertex, $m$ -edge graph, i.e., $O (m \cdot n)$ .

For the soft case of the $𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ constraint where the cost is the minimum number of variables to assign differently in order to get back to a solution, a filtering algorithm achieving arc-consistency is described in [Cymer13], [CymerPhD13]. It has a complexity of $O (p \cdot m)$ , where $p$ is the number of maximal extreme sets in the value graph associated with the constraint and $m$ is the number of edges. It iterates over extreme sets and not over vertices as in the algorithm due to J.-C. Régin.

Reformulation

The $𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ $(𝙽𝙾𝙳𝙴𝚂)$ constraint can be expressed in term of a conjunction of ${| 𝙽𝙾𝙳𝙴𝚂 |}^{2}$ reified constraints of the form $𝙽𝙾𝙳𝙴𝚂 [i] . 𝚜𝚞𝚌𝚌 = j \Leftrightarrow 𝙽𝙾𝙳𝙴𝚂 [j] . 𝚜𝚞𝚌𝚌 = i$ $(1 \leq i, j \leq | 𝙽𝙾𝙳𝙴𝚂 |)$ . The $𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ constraint can also be reformulated as an $𝚒𝚗𝚟𝚎𝚛𝚜𝚎$ constraint as shown below:

𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝 (\begin{matrix} 〈\begin{matrix} 𝚒𝚗𝚍𝚎𝚡 - 1 & 𝚜𝚞𝚌𝚌 - s_{1}, \\ 𝚒𝚗𝚍𝚎𝚡 - 2 & 𝚜𝚞𝚌𝚌 - s_{2}, \\ ⋮ & ⋮ \\ 𝚒𝚗𝚍𝚎𝚡 - n & 𝚜𝚞𝚌𝚌 - s_{n} \end{matrix}〉 \end{matrix})

𝚒𝚗𝚟𝚎𝚛𝚜𝚎 (\begin{matrix} 〈\begin{matrix} 𝚒𝚗𝚍𝚎𝚡 - 1 & 𝚜𝚞𝚌𝚌 - s_{1} & 𝚙𝚛𝚎𝚍 - s_{1}, \\ 𝚒𝚗𝚍𝚎𝚡 - 2 & 𝚜𝚞𝚌𝚌 - s_{2} & 𝚙𝚛𝚎𝚍 - s_{2}, \\ ⋮ & ⋮ & ⋮ \\ 𝚒𝚗𝚍𝚎𝚡 - n & 𝚜𝚞𝚌𝚌 - s_{n} & 𝚙𝚛𝚎𝚍 - s_{n} \end{matrix}〉 \end{matrix})

Counting

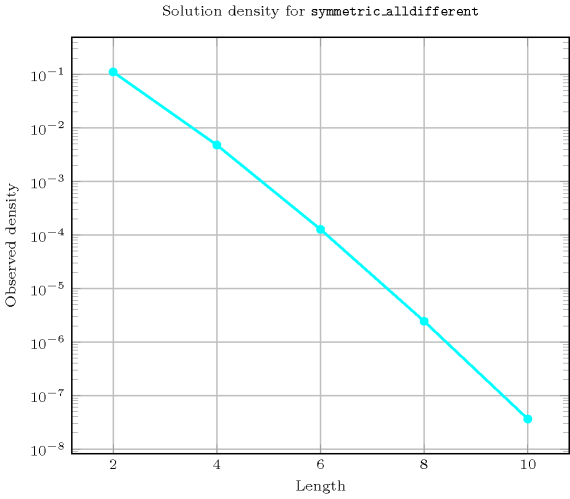
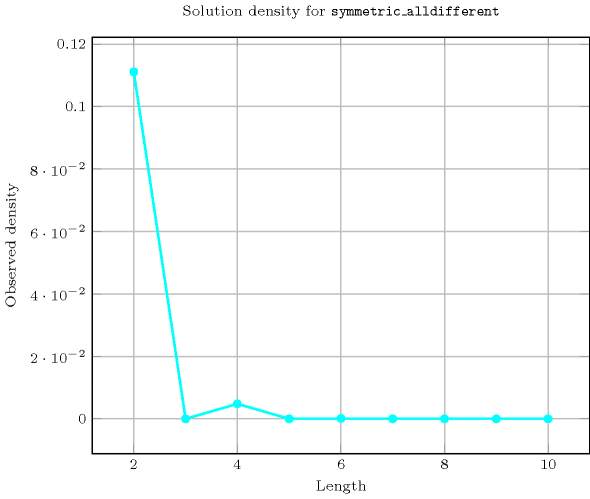
Length ( $n$ )	2	3	4	5	6	7	8	9	10
Solutions	1	0	3	0	15	0	105	0	945

Number of solutions for $𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ : domains $0 . . n$

ctrs/symmetric_alldifferent-2-tikz

ctrs/symmetric_alldifferent-3-tikz

implies: $𝚍𝚎𝚛𝚊𝚗𝚐𝚎𝚖𝚎𝚗𝚝$ , $𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚎𝚡𝚌𝚎𝚙𝚝_0$ , $𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝_𝚕𝚘𝚘𝚙$ .

implies (items to collection): $𝚔_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ , $𝚕𝚎𝚡_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ .

related: $𝚛𝚘𝚘𝚝𝚜$ .

Keywords

application area: sport timetabling.

characteristic of a constraint: all different, disequality.

combinatorial object: permutation, involution, matching.

constraint type: graph constraint, timetabling constraint, graph partitioning constraint.

filtering: arc-consistency.

final graph structure: circuit.

modelling: cycle.

Cond. implications

$•$ $𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝 (𝙽𝙾𝙳𝙴𝚂)$

implies $𝚋𝚊𝚕𝚊𝚗𝚌𝚎_𝚌𝚢𝚌𝚕𝚎$ $(𝙱𝙰𝙻𝙰𝙽𝙲𝙴, 𝙽𝙾𝙳𝙴𝚂)$

when $𝙱𝙰𝙻𝙰𝙽𝙲𝙴 = 0$ .

$•$ $𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝 (𝙽𝙾𝙳𝙴𝚂)$

implies $𝚌𝚢𝚌𝚕𝚎$ $(𝙽𝙲𝚈𝙲𝙻𝙴, 𝙽𝙾𝙳𝙴𝚂)$

when $2 * 𝙽𝙲𝚈𝙲𝙻𝙴 = | 𝙽𝙾𝙳𝙴𝚂 |$ .

$•$ $𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝 (𝙽𝙾𝙳𝙴𝚂)$

implies $𝚙𝚎𝚛𝚖𝚞𝚝𝚊𝚝𝚒𝚘𝚗$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 : 𝙽𝙾𝙳𝙴𝚂)$ .

Arc input(s)

$𝙽𝙾𝙳𝙴𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

(\neq) \mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚗𝚘𝚍𝚎𝚜 1, 𝚗𝚘𝚍𝚎𝚜 2)

Arc arity

Arc constraint(s)

• 𝚗𝚘𝚍𝚎𝚜 1 . 𝚜𝚞𝚌𝚌 = 𝚗𝚘𝚍𝚎𝚜 2 . 𝚒𝚗𝚍𝚎𝚡

• 𝚗𝚘𝚍𝚎𝚜 2 . 𝚜𝚞𝚌𝚌 = 𝚗𝚘𝚍𝚎𝚜 1 . 𝚒𝚗𝚍𝚎𝚡

Graph property(ies)

𝐍𝐀𝐑𝐂

= | 𝙽𝙾𝙳𝙴𝚂 |

Graph model

In order to express the binary constraint that links two vertices one has to make explicit the identifier of the vertices.

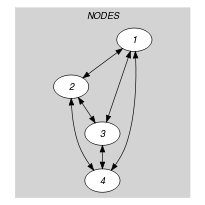
Parts (A) and (B) of Figure 5.395.2 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐀𝐑𝐂$ graph property, the arcs of the final graph are stressed in bold.

Figure 5.395.2. Initial and final graph of the $𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ constraint


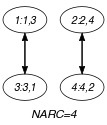
(a)	(b)

Signature

Since all the $𝚒𝚗𝚍𝚎𝚡$ attributes of the $𝙽𝙾𝙳𝙴𝚂$ collection are distinct, and because of the first condition $𝚗𝚘𝚍𝚎𝚜 1 . 𝚜𝚞𝚌𝚌 = 𝚗𝚘𝚍𝚎𝚜 2 . 𝚒𝚗𝚍𝚎𝚡$ of the arc constraint, each vertex of the final graph has at most one successor. Therefore the maximum number of arcs of the final graph is equal to the maximum number of vertices $| 𝙽𝙾𝙳𝙴𝚂 |$ of the final graph. So we can rewrite $𝐍𝐀𝐑𝐂 = | 𝙽𝙾𝙳𝙴𝚂 |$ to $𝐍𝐀𝐑𝐂 \geq | 𝙽𝙾𝙳𝙴𝚂 |$ and simplify $\underset{̲}{\bar{𝐍𝐀𝐑𝐂}}$ to $\bar{𝐍𝐀𝐑𝐂}$ .

Global Constraint Catalog

5. Global Constraint Catalogue

5.395. symmetric_alldifferent

Figure 5.395.1. All solutions corresponding to the non ground example of the 𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝 constraint of the All solutions slot (the 𝚒𝚗𝚍𝚎𝚡 attribute is displayed as indices of the 𝚜𝚞𝚌𝚌 attribute)

Figure 5.395.2. Initial and final graph of the 𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝 constraint

Figure 5.395.2. Initial and final graph of the $𝚜𝚢𝚖𝚖𝚎𝚝𝚛𝚒𝚌_𝚊𝚕𝚕𝚍𝚒𝚏𝚏𝚎𝚛𝚎𝚗𝚝$ constraint