Global Constraint Catalog: Ccumulative_two

5.99. cumulative_two_d

DESCRIPTION

LINKS

Origin

Constraint

$𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎_𝚝𝚠𝚘_𝚍 (𝚁𝙴𝙲𝚃𝙰𝙽𝙶𝙻𝙴𝚂, 𝙻𝙸𝙼𝙸𝚃)$

Arguments

$𝚁𝙴𝙲𝚃𝙰𝙽𝙶𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (\begin{matrix} 𝚜𝚝𝚊𝚛𝚝 1 - 𝚍𝚟𝚊𝚛, \\ 𝚜𝚒𝚣𝚎 1 - 𝚍𝚟𝚊𝚛, \\ 𝚕𝚊𝚜𝚝 1 - 𝚍𝚟𝚊𝚛, \\ 𝚜𝚝𝚊𝚛𝚝 2 - 𝚍𝚟𝚊𝚛, \\ 𝚜𝚒𝚣𝚎 2 - 𝚍𝚟𝚊𝚛, \\ 𝚕𝚊𝚜𝚝 2 - 𝚍𝚟𝚊𝚛, \\ 𝚑𝚎𝚒𝚐𝚑𝚝 - 𝚍𝚟𝚊𝚛 \end{matrix})$
$𝙻𝙸𝙼𝙸𝚃$	$𝚒𝚗𝚝$

Restrictions

𝚛𝚎𝚚𝚞𝚒𝚛𝚎_𝚊𝚝_𝚕𝚎𝚊𝚜𝚝

(2, 𝚁𝙴𝙲𝚃𝙰𝙽𝙶𝙻𝙴𝚂, [𝚜𝚝𝚊𝚛𝚝 1, 𝚜𝚒𝚣𝚎 1, 𝚕𝚊𝚜𝚝 1])

𝚛𝚎𝚚𝚞𝚒𝚛𝚎_𝚊𝚝_𝚕𝚎𝚊𝚜𝚝

(2, 𝚁𝙴𝙲𝚃𝙰𝙽𝙶𝙻𝙴𝚂, [𝚜𝚝𝚊𝚛𝚝 2, 𝚜𝚒𝚣𝚎 2, 𝚕𝚊𝚜𝚝 2])

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚁𝙴𝙲𝚃𝙰𝙽𝙶𝙻𝙴𝚂, 𝚑𝚎𝚒𝚐𝚑𝚝)

𝚁𝙴𝙲𝚃𝙰𝙽𝙶𝙻𝙴𝚂 . 𝚜𝚒𝚣𝚎 1 \geq 0

𝚁𝙴𝙲𝚃𝙰𝙽𝙶𝙻𝙴𝚂 . 𝚜𝚒𝚣𝚎 2 \geq 0

𝚁𝙴𝙲𝚃𝙰𝙽𝙶𝙻𝙴𝚂 . 𝚑𝚎𝚒𝚐𝚑𝚝 \geq 0

𝙻𝙸𝙼𝙸𝚃 \geq 0

Purpose

Consider a set $ℛ$ of rectangles described by the $𝚁𝙴𝙲𝚃𝙰𝙽𝙶𝙻𝙴𝚂$ collection. Enforces that at each point of the plane, the cumulated height of the set of rectangles that overlap that point, does not exceed a given limit.

Example

(\begin{matrix} 〈\begin{matrix} 𝚜𝚝𝚊𝚛𝚝 1 - 1 & 𝚜𝚒𝚣𝚎 1 - 4 & 𝚕𝚊𝚜𝚝 1 - 4 & 𝚜𝚝𝚊𝚛𝚝 2 - 3 & 𝚜𝚒𝚣𝚎 2 - 3 & 𝚕𝚊𝚜𝚝 2 - 5 & 𝚑𝚎𝚒𝚐𝚑𝚝 - 4, \\ 𝚜𝚝𝚊𝚛𝚝 1 - 3 & 𝚜𝚒𝚣𝚎 1 - 2 & 𝚕𝚊𝚜𝚝 1 - 4 & 𝚜𝚝𝚊𝚛𝚝 2 - 1 & 𝚜𝚒𝚣𝚎 2 - 2 & 𝚕𝚊𝚜𝚝 2 - 2 & 𝚑𝚎𝚒𝚐𝚑𝚝 - 2, \\ 𝚜𝚝𝚊𝚛𝚝 1 - 1 & 𝚜𝚒𝚣𝚎 1 - 2 & 𝚕𝚊𝚜𝚝 1 - 2 & 𝚜𝚝𝚊𝚛𝚝 2 - 1 & 𝚜𝚒𝚣𝚎 2 - 2 & 𝚕𝚊𝚜𝚝 2 - 2 & 𝚑𝚎𝚒𝚐𝚑𝚝 - 3, \\ 𝚜𝚝𝚊𝚛𝚝 1 - 4 & 𝚜𝚒𝚣𝚎 1 - 1 & 𝚕𝚊𝚜𝚝 1 - 4 & 𝚜𝚝𝚊𝚛𝚝 2 - 1 & 𝚜𝚒𝚣𝚎 2 - 1 & 𝚕𝚊𝚜𝚝 2 - 1 & 𝚑𝚎𝚒𝚐𝚑𝚝 - 1 \end{matrix}〉, 4 \end{matrix})

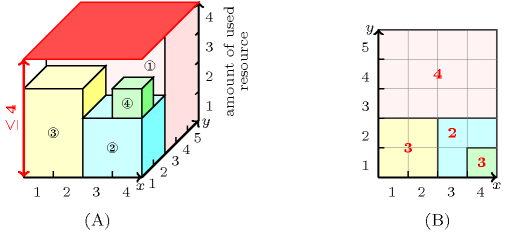
Part (A) of Figure 5.99.1 shows the 4 parallelepipeds of height 4, 2, 3 and 1 associated with the items of the $𝚁𝙴𝙲𝚃𝙰𝙽𝙶𝙻𝙴𝚂$ collection (parallelepipeds since each rectangle also has a height). Part (B) gives the corresponding cumulated 2-dimensional profile, where each number is the cumulated height of all the rectangles that contain the corresponding region. The $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎_𝚝𝚠𝚘_𝚍$ constraint holds since the highest peak of the cumulated 2-dimensional profile does not exceed the upper limit 4 imposed by the last argument of the $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎_𝚝𝚠𝚘_𝚍$ constraint.

Figure 5.99.1. Two representations of a 2-dimensional cumulative profile of the Example slot (where the profile provides for each point of coordinates $(c_{x}, c_{y})$ the corresponding sum of the heights of the items intersecting that point): (A) a three dimensional representation and (B) a two dimensional representation from above with the height of the profile in red; as for the $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ constraint the position of an item on the $z$ axis does not matter, i.e. only its height matters.

Typical

| 𝚁𝙴𝙲𝚃𝙰𝙽𝙶𝙻𝙴𝚂 | > 1

𝚁𝙴𝙲𝚃𝙰𝙽𝙶𝙻𝙴𝚂 . 𝚜𝚒𝚣𝚎 1 > 0

𝚁𝙴𝙲𝚃𝙰𝙽𝙶𝙻𝙴𝚂 . 𝚜𝚒𝚣𝚎 2 > 0

𝚁𝙴𝙲𝚃𝙰𝙽𝙶𝙻𝙴𝚂 . 𝚑𝚎𝚒𝚐𝚑𝚝 > 0

𝙻𝙸𝙼𝙸𝚃 <

𝚜𝚞𝚖

(𝚁𝙴𝙲𝚃𝙰𝙽𝙶𝙻𝙴𝚂 . 𝚑𝚎𝚒𝚐𝚑𝚝)

Symmetries

Items of $𝚁𝙴𝙲𝚃𝙰𝙽𝙶𝙻𝙴𝚂$ are permutable.
Attributes of $𝚁𝙴𝙲𝚃𝙰𝙽𝙶𝙻𝙴𝚂$ are permutable w.r.t. permutation $(𝚜𝚝𝚊𝚛𝚝 1, 𝚜𝚝𝚊𝚛𝚝 2)$ $(𝚜𝚒𝚣𝚎 1, 𝚜𝚒𝚣𝚎 2)$ $(𝚕𝚊𝚜𝚝 1, 𝚕𝚊𝚜𝚝 2)$ $(𝚑𝚎𝚒𝚐𝚑𝚝)$ (permutation applied to all items).
$𝚁𝙴𝙲𝚃𝙰𝙽𝙶𝙻𝙴𝚂 . 𝚑𝚎𝚒𝚐𝚑𝚝$ can be decreased to any value $\geq 0$ .
One and the same constant can be added to the $𝚜𝚝𝚊𝚛𝚝 1$ and $𝚕𝚊𝚜𝚝 1$ attributes of all items of $𝚁𝙴𝙲𝚃𝙰𝙽𝙶𝙻𝙴𝚂$ .
One and the same constant can be added to the $𝚜𝚝𝚊𝚛𝚝 2$ and $𝚕𝚊𝚜𝚝 2$ attributes of all items of $𝚁𝙴𝙲𝚃𝙰𝙽𝙶𝙻𝙴𝚂$ .
$𝙻𝙸𝙼𝙸𝚃$ can be increased.

Arg. properties

Contractible wrt. $𝚁𝙴𝙲𝚃𝙰𝙽𝙶𝙻𝙴𝚂$ .

Usage

The $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎_𝚝𝚠𝚘_𝚍$ constraint is a necessary condition for the $𝚍𝚒𝚏𝚏𝚗$ constraint in 3 dimensions (i.e., the placement of parallelepipeds in such a way that they do not pairwise overlap and that each parallelepiped has his sides parallel to the sides of the placement space).

Algorithm

A first natural way to handle this constraint would be to accumulate the compulsory part [Lahrichi82] of the different rectangles in a quadtree [Samet89]. To each leave of the quadtree we associate the cumulated height of the rectangles containing the corresponding region.

Systems

geost in Choco.

See also

related: $𝚍𝚒𝚏𝚏𝚗$ ( $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎_𝚝𝚠𝚘_𝚍$ is a necessary condition for $𝚍𝚒𝚏𝚏𝚗$ : forget one dimension when the number of dimensions is equal to 3).

specialisation: $𝚋𝚒𝚗_𝚙𝚊𝚌𝚔𝚒𝚗𝚐$ ( $𝚜𝚚𝚞𝚊𝚛𝚎$ of size 1 with a $𝚑𝚎𝚒𝚐𝚑𝚝$ replaced by $𝚝𝚊𝚜𝚔$ of $𝚍𝚞𝚛𝚊𝚝𝚒𝚘𝚗$ 1), $𝚌𝚞𝚖𝚞𝚕𝚊𝚝𝚒𝚟𝚎$ ( $𝚛𝚎𝚌𝚝𝚊𝚗𝚐𝚕𝚎$ with a $𝚑𝚎𝚒𝚐𝚑𝚝$ replaced by $𝚝𝚊𝚜𝚔$ with same $𝚑𝚎𝚒𝚐𝚑𝚝$ ).

Keywords

characteristic of a constraint: derived collection.

constraint type: predefined constraint.

filtering: quadtree, compulsory part.

geometry: geometrical constraint.

Global Constraint Catalog

5. Global Constraint Catalogue

5.99. cumulative_two_d