5.420. weighted_partial_alldiff
| DESCRIPTION | LINKS | GRAPH |
- Origin
- Constraint
- Synonyms
, , .
- Arguments
- Restrictions
- Purpose
All variables of the collection that are not assigned to value must have pairwise distinct values from the attribute of the collection. In addition is the sum of the attributes associated with the values assigned to the variables of . Within the collection, value must be explicitly defined with a weight of 0.
- Example
-
The constraint holds since:
No value, except value , is used more than once.
is equal to the sum of the weights 2, and 7 of the values 1, 2 and 4 assigned to the variables of .
- Typical
- Symmetries
Items of are permutable.
Items of are permutable.
All occurrences of two distinct values in or that are both different from can be swapped; all occurrences of a value in or that is different from can be renamed to any unused value that is also different from .
- Arg. properties
Functional dependency: determined by and .
- Usage
In his PhD thesis [Thiel04], Sven Thiel describes the following three potential scenarios of the constraint:
Given a set of tasks (i.e., the items of the collection), assign to each task a resource (i.e., an item of the collection). Except for the resource associated with value , every resource can be used at most once. The cost of a resource is independent from the task to which the resource is assigned. The cost of value is equal to 0. The total cost of an assignment corresponds to the sum of the costs of the resources effectively assigned to the tasks. Finally we impose an upper bound on the total cost.
Given a set of persons (i.e., the items of the collection), select for each person an offer (i.e., an item of the collection). Except for the offer associated with value , every offer should be selected at most once. The profit associated with an offer is independent from the person that selects the offer. The profit of value is equal to 0. The total benefit is equal to the sum of the profits of the offers effectively selected. In addition we impose a lower bound on the total benefit.
The last scenario deals with an application to an over-constraint problem involving the constraint. Allowing some variables to take an "undefined" value is done by setting all weights of all the values different from to 1. As a consequence all variables assigned to a value different from will have to take distinct values. The variable allows to control the number of such variables.
- Remark
It was shown in [Thiel04] that, finding out whether the constraint has a solution or not is NP-hard. This was achieved by reduction from subset sum.
- Algorithm
A filtering algorithm is given in [Thiel04]. After showing that, deciding whether the has a solution is NP-complete, [Thiel04] gives the following results of his filtering algorithm with respect to consistency under the 3 scenarios previously described:
For scenario 1, if there is no restriction of the lower bound of the variable, the filtering algorithm achieves arc-consistency for all variables of the collection (but not for the variable itself).
For scenario 2, if there is no restriction of the upper bound of the variable, the filtering algorithm achieves arc-consistency for all variables of the collection (but not for the variable itself).
Finally, for scenario 3, the filtering algorithm achieves arc-consistency for all variables of the collection as well as for the variable.
- See also
-
common keyword: (weighted assignment), (cost filtering constraint,weighted assignment), (soft constraint),
- Keywords
-
characteristic of a constraint: all different, joker value.
constraint type: soft constraint, relaxation.
filtering: cost filtering constraint.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph property(ies)
-
- Graph model
Parts (A) and (B) of Figure 5.420.1 respectively show the initial and final graph associated with the Example slot. Since we also use the graph property we show the vertices of the final graph from which we compute the total cost in a box.
Figure 5.420.1. Initial and final graph of the constraint
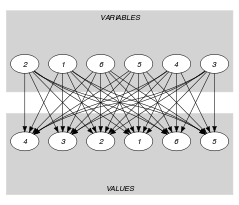
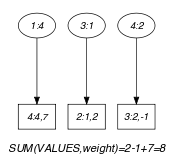
(a) (b)