Global Constraint Catalog: Cbinary

5.55. binary_tree

DESCRIPTION

LINKS

GRAPH

Origin

Derived from $𝚝𝚛𝚎𝚎$ .

Constraint

$𝚋𝚒𝚗𝚊𝚛𝚢_𝚝𝚛𝚎𝚎 (𝙽𝚃𝚁𝙴𝙴𝚂, 𝙽𝙾𝙳𝙴𝚂)$

Arguments

$𝙽𝚃𝚁𝙴𝙴𝚂$	$𝚍𝚟𝚊𝚛$
$𝙽𝙾𝙳𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚒𝚗𝚍𝚎𝚡 - 𝚒𝚗𝚝, 𝚜𝚞𝚌𝚌 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝙽𝚃𝚁𝙴𝙴𝚂 \geq 0

𝙽𝚃𝚁𝙴𝙴𝚂 \leq | 𝙽𝙾𝙳𝙴𝚂 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝙽𝙾𝙳𝙴𝚂, [𝚒𝚗𝚍𝚎𝚡, 𝚜𝚞𝚌𝚌])

𝙽𝙾𝙳𝙴𝚂 . 𝚒𝚗𝚍𝚎𝚡 \geq 1

𝙽𝙾𝙳𝙴𝚂 . 𝚒𝚗𝚍𝚎𝚡 \leq | 𝙽𝙾𝙳𝙴𝚂 |

𝚍𝚒𝚜𝚝𝚒𝚗𝚌𝚝

(𝙽𝙾𝙳𝙴𝚂, 𝚒𝚗𝚍𝚎𝚡)

𝙽𝙾𝙳𝙴𝚂 . 𝚜𝚞𝚌𝚌 \geq 1

𝙽𝙾𝙳𝙴𝚂 . 𝚜𝚞𝚌𝚌 \leq | 𝙽𝙾𝙳𝙴𝚂 |

Purpose

Cover the digraph $G$ described by the $𝙽𝙾𝙳𝙴𝚂$ collection with $𝙽𝚃𝚁𝙴𝙴𝚂$ binary trees in such a way that each vertex of $G$ belongs to exactly one binary tree (i.e., each vertex of $G$ has at most two children). The edges of the binary trees are directed from their leaves to their respective root.

Example

(\begin{matrix} 2, 〈\begin{matrix} 𝚒𝚗𝚍𝚎𝚡 - 1 & 𝚜𝚞𝚌𝚌 - 1, \\ 𝚒𝚗𝚍𝚎𝚡 - 2 & 𝚜𝚞𝚌𝚌 - 3, \\ 𝚒𝚗𝚍𝚎𝚡 - 3 & 𝚜𝚞𝚌𝚌 - 5, \\ 𝚒𝚗𝚍𝚎𝚡 - 4 & 𝚜𝚞𝚌𝚌 - 7, \\ 𝚒𝚗𝚍𝚎𝚡 - 5 & 𝚜𝚞𝚌𝚌 - 1, \\ 𝚒𝚗𝚍𝚎𝚡 - 6 & 𝚜𝚞𝚌𝚌 - 1, \\ 𝚒𝚗𝚍𝚎𝚡 - 7 & 𝚜𝚞𝚌𝚌 - 7, \\ 𝚒𝚗𝚍𝚎𝚡 - 8 & 𝚜𝚞𝚌𝚌 - 5 \end{matrix}〉 \end{matrix})

(\begin{matrix} 8, 〈\begin{matrix} 𝚒𝚗𝚍𝚎𝚡 - 1 & 𝚜𝚞𝚌𝚌 - 1, \\ 𝚒𝚗𝚍𝚎𝚡 - 2 & 𝚜𝚞𝚌𝚌 - 2, \\ 𝚒𝚗𝚍𝚎𝚡 - 3 & 𝚜𝚞𝚌𝚌 - 3, \\ 𝚒𝚗𝚍𝚎𝚡 - 4 & 𝚜𝚞𝚌𝚌 - 4, \\ 𝚒𝚗𝚍𝚎𝚡 - 5 & 𝚜𝚞𝚌𝚌 - 5, \\ 𝚒𝚗𝚍𝚎𝚡 - 6 & 𝚜𝚞𝚌𝚌 - 6, \\ 𝚒𝚗𝚍𝚎𝚡 - 7 & 𝚜𝚞𝚌𝚌 - 7, \\ 𝚒𝚗𝚍𝚎𝚡 - 8 & 𝚜𝚞𝚌𝚌 - 8 \end{matrix}〉 \end{matrix})

(\begin{matrix} 7, 〈\begin{matrix} 𝚒𝚗𝚍𝚎𝚡 - 1 & 𝚜𝚞𝚌𝚌 - 8, \\ 𝚒𝚗𝚍𝚎𝚡 - 2 & 𝚜𝚞𝚌𝚌 - 2, \\ 𝚒𝚗𝚍𝚎𝚡 - 3 & 𝚜𝚞𝚌𝚌 - 3, \\ 𝚒𝚗𝚍𝚎𝚡 - 4 & 𝚜𝚞𝚌𝚌 - 4, \\ 𝚒𝚗𝚍𝚎𝚡 - 5 & 𝚜𝚞𝚌𝚌 - 5, \\ 𝚒𝚗𝚍𝚎𝚡 - 6 & 𝚜𝚞𝚌𝚌 - 6, \\ 𝚒𝚗𝚍𝚎𝚡 - 7 & 𝚜𝚞𝚌𝚌 - 7, \\ 𝚒𝚗𝚍𝚎𝚡 - 8 & 𝚜𝚞𝚌𝚌 - 8 \end{matrix}〉 \end{matrix})

The first $𝚋𝚒𝚗𝚊𝚛𝚢_𝚝𝚛𝚎𝚎$ constraint holds since its second argument corresponds to the 2 (i.e., the first argument of the first $𝚋𝚒𝚗𝚊𝚛𝚢_𝚝𝚛𝚎𝚎$ constraint) binary trees depicted by Figure 5.55.1.

Figure 5.55.1. The two binary trees corresponding to the first example of the Example slot; each vertex contains the information $𝚒𝚗𝚍𝚎𝚡 | 𝚜𝚞𝚌𝚌$ where $𝚜𝚞𝚌𝚌$ is the index of its father in the tree (by convention the father of the root is the root itself).

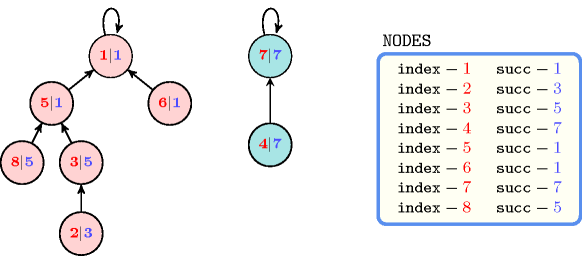
All solutions

Figure 5.55.2 gives all solutions to the following non ground instance of the $𝚋𝚒𝚗𝚊𝚛𝚢_𝚝𝚛𝚎𝚎$ constraint: $𝙽𝚃𝚁𝙴𝙴𝚂 \in {1, 4}$ , $S_{1} \in [1, 2]$ , $S_{2} \in [1, 3]$ , $S_{3} \in [3, 4]$ , $S_{4} \in [3, 4]$ , $S_{5} \in [2, 3]$ , $𝚋𝚒𝚗𝚊𝚛𝚢_𝚝𝚛𝚎𝚎$ $(𝙽𝚃𝚁𝙴𝙴𝚂, 〈 1 S_{1}, 2 S_{2}, 3 S_{3}, 4 S_{4}, 5 S_{5} 〉)$ .

Figure 5.55.2. All solutions corresponding to the non ground example of the $𝚋𝚒𝚗𝚊𝚛𝚢_𝚝𝚛𝚎𝚎$ constraint of the All solutions slot; the $𝚒𝚗𝚍𝚎𝚡$ attribute is displayed as indices of the $𝚜𝚞𝚌𝚌$ attribute and all vertices of a same tree are coloured by the same colour.

Typical

𝙽𝚃𝚁𝙴𝙴𝚂 > 0

𝙽𝚃𝚁𝙴𝙴𝚂 < | 𝙽𝙾𝙳𝙴𝚂 |

| 𝙽𝙾𝙳𝙴𝚂 | > 2

Symmetry

Items of $𝙽𝙾𝙳𝙴𝚂$ are permutable.

Arg. properties

Functional dependency: $𝙽𝚃𝚁𝙴𝙴𝚂$ determined by $𝙽𝙾𝙳𝙴𝚂$ .

Reformulation

The $𝚋𝚒𝚗𝚊𝚛𝚢_𝚝𝚛𝚎𝚎$ constraint can be expressed in term of (1) a set of ${| 𝙽𝙾𝙳𝙴𝚂 |}^{2}$ reified constraints for avoiding circuit between more than one node and of (2) $| 𝙽𝙾𝙳𝙴𝚂 |$ reified constraints and of one sum constraint for counting the trees and of (3) a set of ${| 𝙽𝙾𝙳𝙴𝚂 |}^{2}$ reified constraints and of $| 𝙽𝙾𝙳𝙴𝚂 |$ inequalities constraints for enforcing the fact that each vertex has at most two children.

For each vertex $𝙽𝙾𝙳𝙴𝚂 [i]$ $(i \in [1, | 𝙽𝙾𝙳𝙴𝚂 |])$ of the $𝙽𝙾𝙳𝙴𝚂$ collection we create a variable $R_{i}$ that takes its value within interval $[1, | 𝙽𝙾𝙳𝙴𝚂 |]$ . This variable represents the rank of vertex $𝙽𝙾𝙳𝙴𝚂 [i]$ within a solution. It is used to prevent the creation of circuit involving more than one vertex as explained now. For each pair of vertices $𝙽𝙾𝙳𝙴𝚂 [i], 𝙽𝙾𝙳𝙴𝚂 [j]$ $(i, j \in [1, | 𝙽𝙾𝙳𝙴𝚂 |])$ of the $𝙽𝙾𝙳𝙴𝚂$ collection we create a reified constraint of the form $𝙽𝙾𝙳𝙴𝚂 [i] . 𝚜𝚞𝚌𝚌 = 𝙽𝙾𝙳𝙴𝚂 [j] . 𝚒𝚗𝚍𝚎𝚡 \land i \neq j \Rightarrow R_{i} < R_{j}$ . The purpose of this constraint is to express the fact that, if there is an arc from vertex $𝙽𝙾𝙳𝙴𝚂 [i]$ to another vertex $𝙽𝙾𝙳𝙴𝚂 [j]$ , then $R_{i}$ should be strictly less than $R_{j}$ .
For each vertex $𝙽𝙾𝙳𝙴𝚂 [i]$ $(i \in [1, | 𝙽𝙾𝙳𝙴𝚂 |])$ of the $𝙽𝙾𝙳𝙴𝚂$ collection we create a 0-1 variable $B_{i}$ and state the following reified constraint $𝙽𝙾𝙳𝙴𝚂 [i] . 𝚜𝚞𝚌𝚌 = 𝙽𝙾𝙳𝙴𝚂 [i] . 𝚒𝚗𝚍𝚎𝚡 \Leftrightarrow B_{i}$ in order to force variable $B_{i}$ to be set to value 1 if and only if there is a loop on vertex $𝙽𝙾𝙳𝙴𝚂 [i]$ . Finally we create a constraint $𝙽𝚃𝚁𝙴𝙴𝚂 = B_{1} + B_{2} + \dots + B_{| 𝙽𝙾𝙳𝙴𝚂 |}$ for stating the fact that the number of trees is equal to the number of loops of the graph.
For each pair of vertices $𝙽𝙾𝙳𝙴𝚂 [i], 𝙽𝙾𝙳𝙴𝚂 [j]$ $(i, j \in [1, | 𝙽𝙾𝙳𝙴𝚂 |])$ of the $𝙽𝙾𝙳𝙴𝚂$ collection we create a 0-1 variable $B_{i j}$ and state the following reified constraint $𝙽𝙾𝙳𝙴𝚂 [i] . 𝚜𝚞𝚌𝚌 = 𝙽𝙾𝙳𝙴𝚂 [j] . 𝚒𝚗𝚍𝚎𝚡 \land i \neq j \Leftrightarrow B_{i j}$ . Variable $B_{i j}$ is set to value 1 if and only if there is an arc from $𝙽𝙾𝙳𝙴𝚂 [i]$ to $𝙽𝙾𝙳𝙴𝚂 [j]$ . Then for each vertex $𝙽𝙾𝙳𝙴𝚂 [j]$ $(j \in [1, | 𝙽𝙾𝙳𝙴𝚂 |])$ we create a constraint of the form $B_{1 j} + B_{2 j} + \dots + B_{| 𝙽𝙾𝙳𝙴𝚂 | j} \leq 2$ .

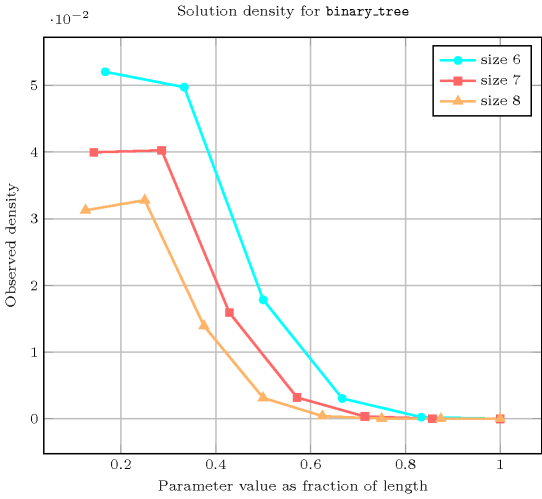
Counting

Length ( $n$ )	2	3	4	5	6	7	8
Solutions	3	16	121	1191	14461	209098	3510921

Number of solutions for $𝚋𝚒𝚗𝚊𝚛𝚢_𝚝𝚛𝚎𝚎$ : domains $0 . . n$

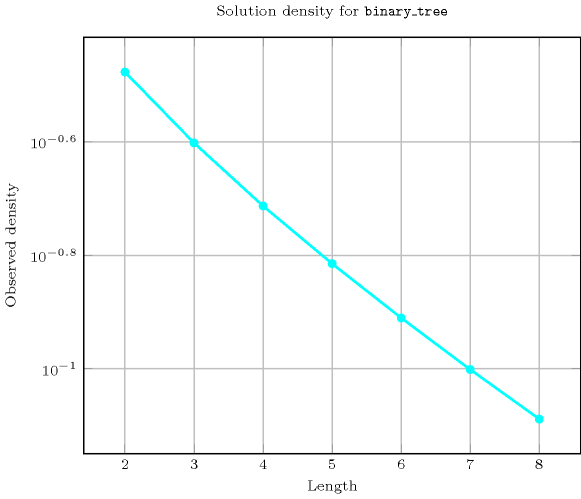
ctrs/binary_tree-3-tikz

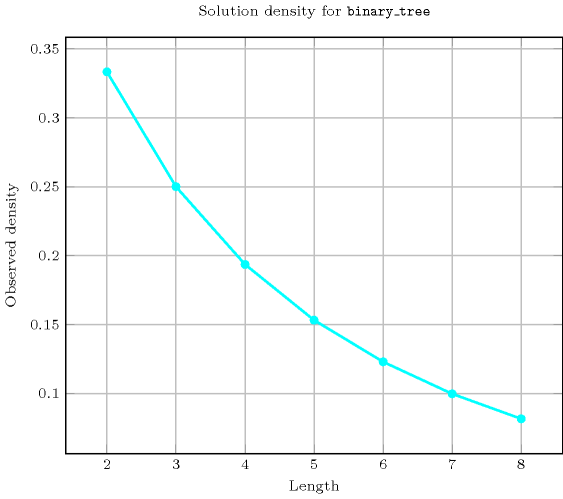
ctrs/binary_tree-4-tikz

Length (

n

)

Total

121

1191

14461

209098

3510921

Parameter

value

540

6120

83790

1345680

480

5850

84420

1411200

150

2100

33390

599760

360

6720

135240

735

17640

1344

Solution count for $𝚋𝚒𝚗𝚊𝚛𝚢_𝚝𝚛𝚎𝚎$ : domains $0 . . n$

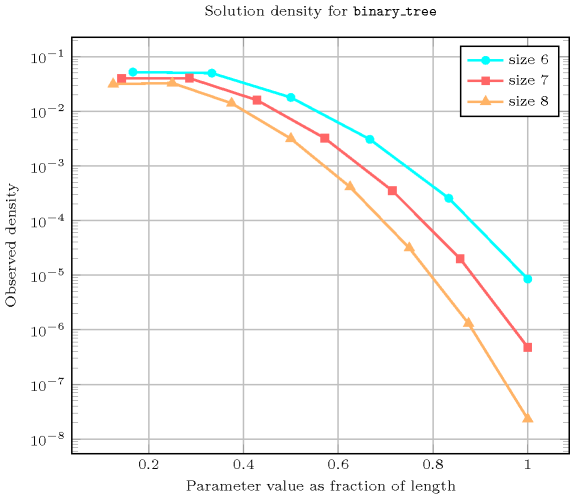
ctrs/binary_tree-5-tikz

ctrs/binary_tree-6-tikz

See also

generalisation: $𝚝𝚛𝚎𝚎$ (at most two childrens replaced by no restriction on maximum number of childrens).

implied by: $𝚙𝚊𝚝𝚑$ .

implies: $𝚝𝚛𝚎𝚎$ .

implies (items to collection): $𝚊𝚝𝚕𝚎𝚊𝚜𝚝_𝚗𝚟𝚎𝚌𝚝𝚘𝚛$ .

specialisation: $𝚙𝚊𝚝𝚑$ (at most two childrens replaced by at most one child).

Keywords

constraint type: graph constraint, graph partitioning constraint.

final graph structure: connected component, tree, one_succ.

modelling: functional dependency.

Arc input(s)

$𝙽𝙾𝙳𝙴𝚂$

Arc generator

𝐶𝐿𝐼𝑄𝑈𝐸

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚗𝚘𝚍𝚎𝚜 1, 𝚗𝚘𝚍𝚎𝚜 2)

Arc arity

Arc constraint(s)

𝚗𝚘𝚍𝚎𝚜 1 . 𝚜𝚞𝚌𝚌 = 𝚗𝚘𝚍𝚎𝚜 2 . 𝚒𝚗𝚍𝚎𝚡

Graph property(ies)

•

𝐌𝐀𝐗_𝐍𝐒𝐂𝐂

\leq 1

•

𝐍𝐂𝐂

= 𝙽𝚃𝚁𝙴𝙴𝚂

•

𝐌𝐀𝐗_𝐈𝐃

\leq 2

Graph class

𝙾𝙽𝙴_𝚂𝚄𝙲𝙲

Graph model

We use the same graph constraint as for the $𝚝𝚛𝚎𝚎$ constraint, except that we add the graph property $𝐌𝐀𝐗_𝐈𝐃$ $\leq$ 2, which constraints the maximum in-degree of the final graph to not exceed 2. $𝐌𝐀𝐗_𝐈𝐃$ does not consider loops: This is why we do not have any problem with the root of each tree.

Parts (A) and (B) of Figure 5.55.3 respectively show the initial and final graph associated with the first example of the Example slot. Since we use the $𝐍𝐂𝐂$ graph property, we display the two connected components of the final graph. Each of them corresponds to a binary tree. Since we use the $𝐌𝐀𝐗_𝐈𝐍_𝐃𝐄𝐆𝐑𝐄𝐄$ graph property, we also show with a double circle a vertex that has a maximum number of predecessors.

The $𝚋𝚒𝚗𝚊𝚛𝚢_𝚝𝚛𝚎𝚎$ constraint holds since all strongly connected components of the final graph have no more than one vertex, since $𝙽𝚃𝚁𝙴𝙴𝚂$ $=$ $𝐍𝐂𝐂$ $=$ 2 and since $𝐌𝐀𝐗_𝐈𝐃$ $=$ 2.

Figure 5.55.3. Initial and final graph of the $𝚋𝚒𝚗𝚊𝚛𝚢_𝚝𝚛𝚎𝚎$ constraint


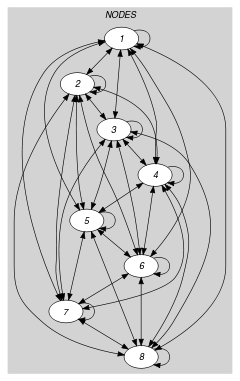
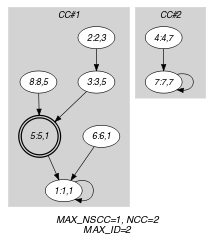
(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.55. binary_tree

Figure 5.55.1. The two binary trees corresponding to the first example of the Example slot; each vertex contains the information 𝚒𝚗𝚍𝚎𝚡|𝚜𝚞𝚌𝚌 where 𝚜𝚞𝚌𝚌 is the index of its father in the tree (by convention the father of the root is the root itself).

Figure 5.55.3. Initial and final graph of the 𝚋𝚒𝚗𝚊𝚛𝚢_𝚝𝚛𝚎𝚎 constraint

Figure 5.55.1. The two binary trees corresponding to the first example of the Example slot; each vertex contains the information $𝚒𝚗𝚍𝚎𝚡 | 𝚜𝚞𝚌𝚌$ where $𝚜𝚞𝚌𝚌$ is the index of its father in the tree (by convention the father of the root is the root itself).

Figure 5.55.3. Initial and final graph of the $𝚋𝚒𝚗𝚊𝚛𝚢_𝚝𝚛𝚎𝚎$ constraint