Global Constraint Catalog: Camong

5.29. among_var

DESCRIPTION

LINKS

GRAPH

Origin

Generalisation of $𝚊𝚖𝚘𝚗𝚐$

Constraint

$𝚊𝚖𝚘𝚗𝚐_𝚟𝚊𝚛 (𝙽𝚅𝙰𝚁, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚅𝙰𝙻𝚄𝙴𝚂)$

Arguments

$𝙽𝚅𝙰𝚁$	$𝚍𝚟𝚊𝚛$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚅𝙰𝙻𝚄𝙴𝚂$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚕 - 𝚍𝚟𝚊𝚛)$

Restrictions

𝙽𝚅𝙰𝚁 \geq 0

𝙽𝚅𝙰𝚁 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂, 𝚟𝚊𝚛)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝙻𝚄𝙴𝚂, 𝚟𝚊𝚕)

Purpose

$𝙽𝚅𝙰𝚁$ is the number of variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ that are equal to one of the variables of the collection $𝚅𝙰𝙻𝚄𝙴𝚂$ .

Example

(3, 〈4, 5, 5, 4, 1〉, 〈1, 5, 8, 1〉)

The $𝚊𝚖𝚘𝚗𝚐_𝚟𝚊𝚛$ constraint holds since exactly 3 values of the collection of variables $〈 4, 5, 5, 4, 1 〉$ occurs within the collection $〈 1, 5, 8, 1 〉$ .

Typical

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > 1

| 𝚅𝙰𝙻𝚄𝙴𝚂 | > 1

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 | > | 𝚅𝙰𝙻𝚄𝙴𝚂 |

Symmetries

Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ are permutable.
Items of $𝚅𝙰𝙻𝚄𝙴𝚂$ are permutable.
All occurrences of two distinct values in $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ or $𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕$ can be swapped; all occurrences of a value in $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ or $𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕$ can be renamed to any unused value.
An occurrence of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 . 𝚟𝚊𝚛$ that belongs to $𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕$ (resp. does not belong to $𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕$ ) can be replaced by any other value in $𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕$ (resp. not in $𝚅𝙰𝙻𝚄𝙴𝚂 . 𝚟𝚊𝚕$ ).

Arg. properties

Functional dependency: $𝙽𝚅𝙰𝚁$ determined by $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ and $𝚅𝙰𝙻𝚄𝙴𝚂$ .
Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ when $𝙽𝚅𝙰𝚁 = 0$ .
Contractible wrt. $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ when $𝙽𝚅𝙰𝚁 = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 |$ .
Aggregate: $𝙽𝚅𝙰𝚁 (+)$ , $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 (𝚞𝚗𝚒𝚘𝚗)$ , $𝚅𝙰𝙻𝚄𝙴𝚂 (𝚞𝚗𝚒𝚘𝚗)$ .

Systems

among in Choco, count in Gecode, amongvar in JaCoP.

See also

implied by: $𝚊𝚖𝚘𝚗𝚐$ .

related: $𝚌𝚘𝚖𝚖𝚘𝚗$ .

specialisation: $𝚊𝚖𝚘𝚗𝚐$ ( $𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎$ replaced by $𝚌𝚘𝚗𝚜𝚝𝚊𝚗𝚝$ within list of $𝚟𝚊𝚕𝚞𝚎𝚜$ $𝚅𝙰𝙻𝚄𝙴𝚂$ ).

uses in its reformulation: $𝚖𝚒𝚗_𝚗$ .

Keywords

constraint arguments: pure functional dependency.

constraint type: counting constraint.

final graph structure: acyclic, bipartite, no loop.

modelling: functional dependency.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂$ $𝚅𝙰𝙻𝚄𝙴𝚂$

Arc generator

𝑃𝑅𝑂𝐷𝑈𝐶𝑇

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜, 𝚟𝚊𝚕𝚞𝚎𝚜)

Arc arity

Arc constraint(s)

𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 . 𝚟𝚊𝚛 = 𝚟𝚊𝚕𝚞𝚎𝚜 . 𝚟𝚊𝚕

Graph property(ies)

𝐍𝐒𝐎𝐔𝐑𝐂𝐄

= 𝙽𝚅𝙰𝚁

Graph class

•

𝙰𝙲𝚈𝙲𝙻𝙸𝙲

•

𝙱𝙸𝙿𝙰𝚁𝚃𝙸𝚃𝙴

•

𝙽𝙾_𝙻𝙾𝙾𝙿

Graph model

Parts (A) and (B) of Figure 5.29.1 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐒𝐎𝐔𝐑𝐂𝐄$ graph property, the source vertices of the final graph are stressed with a double circle. Since the final graph has only 3 sources the variables $𝙽𝚅𝙰𝚁$ is fixed to 3.

Figure 5.29.1. Initial and final graph of the $𝚊𝚖𝚘𝚗𝚐_𝚟𝚊𝚛$ constraint


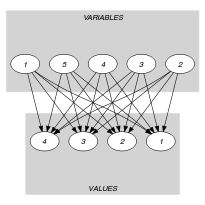
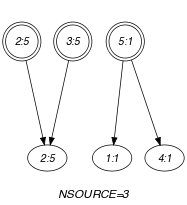
(a)	(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.29. among_var

Figure 5.29.1. Initial and final graph of the 𝚊𝚖𝚘𝚗𝚐_𝚟𝚊𝚛 constraint

Figure 5.29.1. Initial and final graph of the $𝚊𝚖𝚘𝚗𝚐_𝚟𝚊𝚛$ constraint