5.144. element_sparse
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
CHIP
- Constraint
- Usual name
- Arguments
- Restrictions
- Purpose
is equal to one of the entries of the table or to the default value if the entry does not exist in .
- Example
-
The constraint holds since its first argument corresponds to the second item of the collection.
- Typical
- Symmetries
Items of are permutable.
All occurrences of two distinct values in , or can be swapped; all occurrences of a value in , or can be renamed to any unused value.
- Usage
A sometimes more compact form of the constraint: we are not obliged to specify explicitly the table entries that correspond to the specified default value. This can sometimes reduce drastically memory utilisation.
- Remark
The original constraint of CHIP had an additional parameter giving the maximum value of .
- Reformulation
Let and respectively denote and . The constraint can be expressed in term of a reified constraint of the form:
.
- See also
common keyword: , (array constraint), (sparse table).
implies: .
- Keywords
characteristic of a constraint: automaton, automaton without counters, reified automaton constraint, derived collection.
constraint arguments: binary constraint.
constraint network structure: centered cyclic(2) constraint network(1).
constraint type: data constraint.
modelling: array constraint, table, sparse table, sparse functional dependency, variable indexing.
- Derived Collections
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph property(ies)
-
- Graph model
The final graph has between one and two arc constraints: it has two arcs when the default value occurs also in the table ; otherwise it has only one arc.
Parts (A) and (B) of Figure 5.144.1 respectively show the initial and final graph associated with the Example slot. Since we use the graph property the arcs of the final graph are outline with thick lines.
Figure 5.144.1. Initial and final graph of the constraint
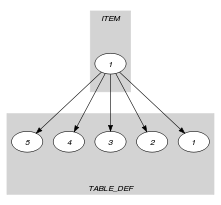
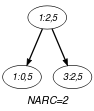
(a) (b)
- Automaton
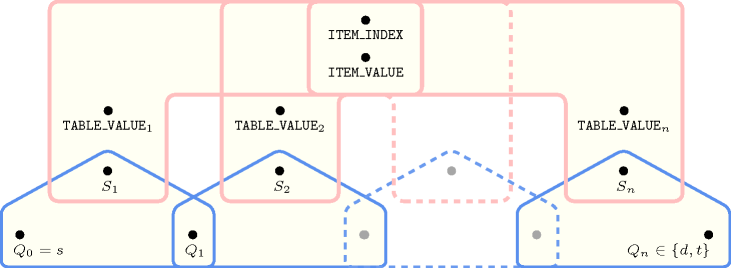
Figure 5.144.2 depicts the automaton associated with the constraint. Let and respectively be the and the attributes of the unique item of the collection. Let and respectively be the and the attributes of the item of the collection. To each quintuple corresponds a signature variable as well as the following signature constraint:
.
Figure 5.144.2. Automaton of the constraint
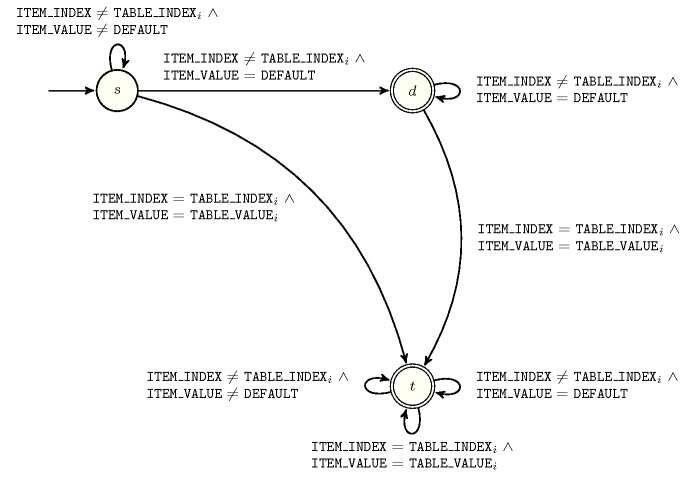
Figure 5.144.3. Hypergraph of the reformulation corresponding to the automaton of the constraint